【题目】如图,在Rt△ABC,∠C=90°,AC=12,BC=6,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,要使△ABC和△QPA全等,则AP= 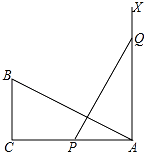
参考答案:
【答案】6或12
【解析】解:①当AP=CB时,∵∠C=∠QAP=90°,
在Rt△ABC与Rt△QPA中, ![]() ,
,
∴Rt△ABC≌Rt△QPA(HL),
即AP=BC=6;
②当P运动到与C点重合时,AP=AC,
在Rt△ABC与Rt△QPA中, ![]() ,
,
∴Rt△QAP≌Rt△BCA(HL),
即AP=AC=12,
∴当点P与点C重合时,△ABC才能和△APQ全等.
综上所述,AP=6或12.
故答案为:6或12.
本题要分情况讨论:①Rt△APQ≌Rt△CBA,此时AP=BC=6,可据此求出P点的位置.②Rt△QAP≌Rt△BCA,此时AP=AC=12,P、C重合.
-
科目: 来源: 题型:
查看答案和解析>>【题目】当下共享单车在各大城市相当火热,给人们的短距离出行带来了许多便利.某市准备在2017年分四期投放若干辆“飞歌同程”和“摩拜单车”两种品牌的共享单车.决策人员根据计划绘制了如图所示的两幅统计图.
(1)第四期投放占总量的百分比是 ;
(2)计算该市四期共投放多少辆共享单车;
(3)补全四期投放共享单车折线统计图.


-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=2017(x﹣20)2+18的顶点坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请写出一个开口向上,且对称轴为直线x=3的二次函数解析式_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)3ab2(﹣
 a2b)2abc;
a2b)2abc;(2)(﹣
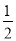 x2y)3(﹣3xy2);
x2y)3(﹣3xy2);(3)(﹣3xy2)3(
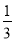 x3y);
x3y);(4)(x2+3x)﹣2(4x﹣x2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点C在直线AB上,AC=8cm,BC=6cm,点M、N分别是AC、BC的中点,求线段MN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一种商品进价为每件100元,按进价增加20%出售,后因库存积压降价,按售价的九折出售,每件还能盈利( )
A. 8元B. 15元C. 12.5元D. 108元
相关试题

