【题目】如图,射线OA∥射线CB,∠C=∠OAB=100°.点D、E在线段CB上,且∠DOB=∠BOA, OE平分∠DOC.
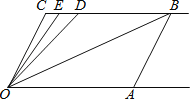
(1)试说明AB∥OC的理由;
(2)试求∠BOE的度数;
(3)平移线段AB;
①试问∠OBC:∠ODC的值是否会发生变化?若不会,请求出这个比值;若会,请找出相应变化规律.
②若在平移过程中存在某种情况使得∠OEC=∠OBA,试求此时∠OEC的度数.
参考答案:
【答案】(1)答案见解析 (2)∠BOE=40°. (3)①不会,比值=1:2;②∠OEC=60°.
【解析】
试题分析:(1)根据OA//CB,得出![]() ,再根据已知条件,即可证明∠C+∠ABC=180°,从而得证.(2)根据两直线平行,同旁内角互补求出∠AOC,再求出∠EOB=
,再根据已知条件,即可证明∠C+∠ABC=180°,从而得证.(2)根据两直线平行,同旁内角互补求出∠AOC,再求出∠EOB=![]() ∠AOC.(3)①根据两直线平行,内错角相等可得∠AOB=∠OBC,再根据三角形的外角性质∠OEC=2∠OBC即可.②根据三角形的内角定理,求出∠COE=∠AOB,从而得到OB、OD、OE是∠AOC的四等分线,在利用三角形的内角定理即可求出∠OEC的度数.
∠AOC.(3)①根据两直线平行,内错角相等可得∠AOB=∠OBC,再根据三角形的外角性质∠OEC=2∠OBC即可.②根据三角形的内角定理,求出∠COE=∠AOB,从而得到OB、OD、OE是∠AOC的四等分线,在利用三角形的内角定理即可求出∠OEC的度数.
试题解析:(1)∵OA∥CB,∴∠OAB+∠ABC=180°,∵∠C=∠OAB=100°,∴∠C+∠ABC=180°,
∴AB∥OC . (2)∵CB∥OA,∴∠AOC=180°﹣∠C=180°﹣100°=80°,∵OE平分∠COD,∴∠COE=∠EOD,∵∠DOB=∠AOB,∴∠EOB=∠EOD+∠DOB=![]() ∠AOC=
∠AOC=![]() ×80°=40°;(3)①∵CB∥OA,∴∠AOB=∠OBC,∵∠EOB=∠AOB,∴∠EOB=∠OBC,∴∠OEC=∠EOB+∠OBC=2∠OBC,∴∠OBC:∠OEC=1:2,是定值;
×80°=40°;(3)①∵CB∥OA,∴∠AOB=∠OBC,∵∠EOB=∠AOB,∴∠EOB=∠OBC,∴∠OEC=∠EOB+∠OBC=2∠OBC,∴∠OBC:∠OEC=1:2,是定值;
②在△COE和△AOB中,∵∠OEC=∠OBA,∠C=∠OAB,∴∠COE=∠AOB,∴OB、OD、OE是∠AOC的四等分线,
∴∠COE=![]() ∠AOC=
∠AOC=![]() ×80°=20°,∴∠OEC=180°﹣∠C﹣∠COE=180°﹣100°﹣20°=60°,∴∠OEC=∠OBA,此时∠OEC=∠OBA=60°.
×80°=20°,∴∠OEC=180°﹣∠C﹣∠COE=180°﹣100°﹣20°=60°,∴∠OEC=∠OBA,此时∠OEC=∠OBA=60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD对折,使它落在斜边AB上,且与AE重合,求CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在10×10网格中,每个小方格的边长看做单位1,每个小方格的顶点叫做格点,△ABC的顶点都在格点上.

(1)请在网格中画出△ABC的一个位似图形△A1B1C1,使两个图形以点C为位似中心,且所画图形与△ABC的位似比为2:1;
(2)将△A1B1C1绕着点C1顺时针旋转90°得△A2B2C2,画出图形,并分别写出△A2B2C2三个顶点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中, A、B两点分别在x轴、y轴的正半轴上,且OB = OA=3.
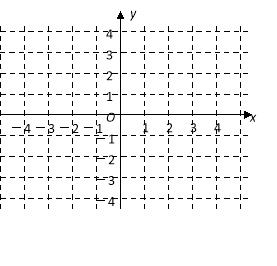
(1)、求点A、B的坐标;(2)、已知点C(-2,2),求△BOC的面积; (3)、点P是第一象限角平分线上一点,若
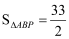 ,求点P的坐标.
,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠C=90°,AC=3,BC=4,D是AB上一动点(不与A、B重合),DE⊥AC于点E,DF⊥BC于点F,点D由A向B移动时,矩形DECF的周长变化情况是( )
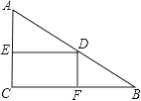
A. 逐渐减小 B. 逐渐增大 C. 先增大后减小 D. 先减小后增大
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公交车原坐有22人,经过3个站点时上下车情况如下(上车为正,下车为负):(+4,8),(5,6),(3,2),则车上还有________人.
-
科目: 来源: 题型:
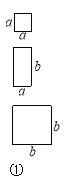
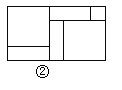
查看答案和解析>>【题目】一天,小明和小玲玩纸片拼图游戏,发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式。比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2.
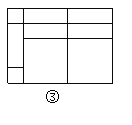
(1)图③可以解释为等式:
(2)要使拼出的矩形面积为3a2+8ab+4b2,则此矩形的长为 ,宽为 .
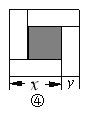
(3)如图④,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个矩形的两边长(x>y),观察图案,指出以下关系式
Ⅰ.
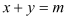 Ⅱ.x-y=n Ⅲ.
Ⅱ.x-y=n Ⅲ.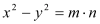 Ⅳ
Ⅳ
Ⅴ.
 其中正确的有几个( )
其中正确的有几个( )A.2个 B.3个 C.4个 D.5个
(4)如图5,是将两个边长分别为
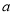 和
和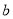 的正方形拼在一起,B、C、G三点在同一直线上,连接BD和BF,若两正方形的边长满足a+b=6,ab=6,你能求出阴影部分的面积S阴 吗?
的正方形拼在一起,B、C、G三点在同一直线上,连接BD和BF,若两正方形的边长满足a+b=6,ab=6,你能求出阴影部分的面积S阴 吗?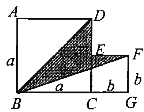
相关试题

