Question

【题目】在正方形中，是上的一动点，连接，分别过点作，垂足为.

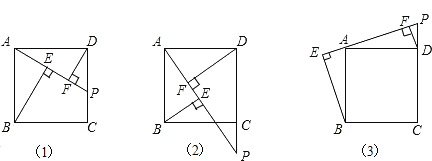
（1）求证：；

（2）如图（2），若点是的延长线上的一个动点，请探索三条线段之间的数量关系？并说明理由；

（3）如图（3），若点是的延长线上的一个动点，请探索三条线之间的数量关系？（直接写出结论，不需说明理由）

Answer 1

【答案】（1）BE=EF+DF；（2）DF=EF+BE；（3）EF=BE+DF．

【解析】

试题解析：（1）根据正方形的性质可知证出△ABE≌△DAF，根据全等三角形的性质：全等三角形对应边相等可得：BE=AF，AE=DF，得出BE=EF+DF；

（2）同（1）的证法相同，先证明△ABE≌△DAF，利用全等三角形的性质可得：BE=AF，BE=DF，再根据等量代换可得出图（2）中DF=EF+BE；

（3）同（1）的证法相同，可得出图（3）中EF=EB+FD．

试题解析：（1）BE=EF+DF，

证明：∵BE⊥PA，DF⊥PA，

∴∠BEA=∠AFD=90°，

∵四边形ABCD是正方形，

∴AB=AD，∠BAD=90°，

∴∠BAE+∠DAF=∠ADF+∠DAF=90°，

∴∠BAE=∠ADF，

在△BAE和△ADF中

，

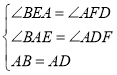∴△BAE≌△ADF（AAS），

∴BE=AF，AE=DF，

∵AF-AE=EF，

∴BE-DF=EF．

（2）DF=BE+EF，

证明：∵四边形ABCD是正方形，

∴AB=AD，∠BAE+∠DAF=90°，

∵BE⊥PA、DF⊥PA，

∴∠AEB=∠DFA=90°，

∴∠BAE+∠ABE=90°，

∴∠ABE=∠DAF，

在△ABE和△DAF中，

，

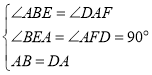∴△ABE≌△DAF（AAS），

∴BE=AF，AE=DF，

∵AE=AF+EF，

∴DF=EB+EF．

（3）EF=BE+DF．

证明：∵四边形ABCD是正方形，

∴AB=AD，∠BAD=90°，

∴∠1+∠3=90°，

∵BE⊥PA、DF⊥PA，

∴∠AEB=∠DFA=90°，

∴∠2+∠3=90°，

∴∠1=∠2，

在△ABE和△DAF中，

，

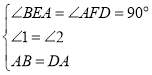∴△ABE≌△DAF（AAS），

∴BE=AF，AE=DF（全等三角形对应边相等），

∵EF=AF+AE，

∴EF=EB+FD（等量代换）．