【题目】课堂上,老师给出了如下一道探究题:“如图,在边长为1的正方形组成的6×8的方格中,△ABC和△A1B1C1的顶点都在格点上,且△ABC≌△A1B1C1 . 请利用平移或旋转变换,设计一种方案,使得△ABC通过一次或两次变换后与△A1B1C1完全重合.”
(1)小明的方案是:“先将△ABC向右平移两个单位得到△A2B2C2 , 再通过旋转得到△A1B1C1”.请根据小明的方案画出△A2B2C2 , 并描述旋转过程;
(2)小红通过研究发现,△ABC只要通过一次旋转就能得到△A1B1C1 . 请在图中标出小红方案中的旋转中心P,并简要说明你是如何确定的.
参考答案:
【答案】
(1)
解:如图所示,△A2B2C2即为所求,将△A2B2C2绕着点B1顺时针旋转90°,即可得到△A1B1C1.

(2)
解:如图所示,连接CC1,BB1,作CC1的垂直平分线,BB1的垂直平分线,交于点P,则点P即为旋转中心.

【解析】(1)根据平移的方向和距离,即可得到△A2B2C2 , 将△A2B2C2绕着点B1顺时针旋转90°,即可得到△A1B1C1 .
(2)连接CC1 , BB1 , 作CC1的垂直平分线,BB1的垂直平分线,交于点P,根据对应点到旋转中心的距离相等,即可得到点P即为旋转中心.
-
科目: 来源: 题型:
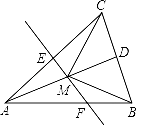
查看答案和解析>>【题目】如图,已知△ABC,AB=AC,AD是△ABC的角平分线,EF垂直平分AC,分别交AC,AD,AB于点E,M,F.若∠CAD=20°,求∠MCD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①一条直线有且只有一条垂线;②画出点P到直线l的距离;③两条直线相交就是垂直;④线段和射线也有垂线,其中正确的有_____;
-
科目: 来源: 题型:
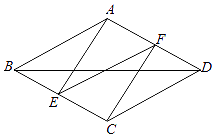
查看答案和解析>>【题目】如图,已知菱形ABCD,AB=5,对角线BD=8,作AE⊥BC于点E,CF⊥AD于点F,连接EF,求EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 互补的两个角是邻补角 B. 两直线平行,同旁内角相等
C. “同旁内角互补”不是命题 D. “相等的两个角是对顶角”是假命题
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2×106)3=( )
A.6×109
B.8×109
C.2×1018
D.8×1018 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形的边OA在x轴上,边OC在y轴上,点B的坐标为(10,8),沿直线OD折叠矩形,使点A正好落在BC上的E处,E点坐标为(6,8),抛物线
 经过O、A、E三点.
经过O、A、E三点.(1)求此抛物线的解析式;
(2)求AD的长;
(3)点P是抛物线对称轴上的一动点,当△PAD的周长最小时,求点P的坐标.

相关试题

