【题目】已知, ![]() 、
、![]() 均为等边三角形,点
均为等边三角形,点![]() 是
是![]() 内的点
内的点
(1)如图①,说明![]() 的理由;
的理由;

(2)如图②,当点![]() 在线段
在线段![]() 上时,求
上时,求![]() 的度数;
的度数;

(3)当![]() 为等腰直角三角形时,
为等腰直角三角形时,![]() ________度(直接写出客案).
________度(直接写出客案).
参考答案:
【答案】(1)见解析;(2)见解析;(3)![]() 或
或![]() 或
或![]() .
.
【解析】
(1)先理由等边三角形的性质得出![]() ,
,![]() ,
,![]() ,即可得出结论;
,即可得出结论;
(2)同(1)得![]() ,再判断出
,再判断出![]() ,进而求出
,进而求出![]() ,即可得出结论;
,即可得出结论;
(3)当![]() 为等腰直角三角形时,有三种情况:I.当∠EDB=90°,DE=DB时, II.当∠BED=90°,BE=DB时,当∠EDB=90°,DE=DB时,分别作出图形,然后根据等腰三角形性质即可求出.
为等腰直角三角形时,有三种情况:I.当∠EDB=90°,DE=DB时, II.当∠BED=90°,BE=DB时,当∠EDB=90°,DE=DB时,分别作出图形,然后根据等腰三角形性质即可求出.
解:(1)∵![]() 和
和![]() 都是等边三角形(已知)
都是等边三角形(已知)
∴![]() ,
,![]() ,
,![]() (等边三角形的性质)。
(等边三角形的性质)。
∴![]() (等式性质),即
(等式性质),即![]() ,
,
在![]() 和
和![]() 中,
中,
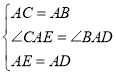 ,
,
∴![]()
∴![]() (全等三角形对应边相等)
(全等三角形对应边相等)
(2)∵![]() 是等边三角形(已知)。
是等边三角形(已知)。
∴![]() (等边三角形的性质)。
(等边三角形的性质)。
∴![]() (邻补角的意义)
(邻补角的意义)
∴![]() (等式性质)
(等式性质)
∴同理(1)得![]()
∴![]() (全等三角形对应角相等)
(全等三角形对应角相等)
∴![]() (等式性质)
(等式性质)
(3)当![]() 为等腰直角三角形时,有三种情况:
为等腰直角三角形时,有三种情况:
I.当∠EDB=90°,DE=DB时,如图③-1:

∵∠ADE=60°,
∴∠ADB=∠ADE+∠EDB=60°+90°=150°,
又∵AD=DE,
∴AD=BD,
∴∠DAB=∠ABD=![]() ;
;
II.当∠BED=90°,BE=DB时,如图③-2:
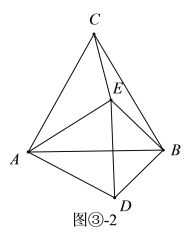
在△ABE和△ADB中:
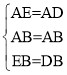 ,
,
∴△ABE≌△ADB(SSS)
∴∠ABE=∠ABD,
∴ ![]() ;
;
III.当∠EDB=90°,DE=DB时,如图③-3:

同I可得:∠ABE=15°,
∵∠EBD=![]() ,
,
∴∠ABD=![]() .
.
综上所述:∠ABD=![]() 或
或![]() 或
或![]() .
.
故答案为:![]() 或
或![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】4月23日是“世界读书日”,学校开展“让书香溢满校园”读书活动,以提升青少年的阅读兴趣,九年级(1)班数学活动小组对本年级600名学生每天阅读时间进行了统计,根据所得数据绘制了两幅不完整统计图(每组包括最小值不包括最大值).九年级(1)班每天阅读时间在0.5小时以内的学生占全班人数的8%.根据统计图解答下列问题:

(1)九年级(1)班有 名学生;
(2)补全直方图;
(3)除九年级(1)班外,九年级其他班级每天阅读时间在1~1.5小时的学生有165人,请你补全扇形统计图;
(4)求该年级每天阅读时间不少于1小时的学生有多少人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在研究气体压强和体积关系的物理实验中,一个气球内充满了一定质量的气体,实验中气体温度保持不变,实验人员记录了实验过程中气球内的气体压强p(kPa)与气体体积V(m3)的数据如下表:
V(m3)
0.8
1.2
1.6
2.0
2.4
p(kPa)
120
80
60
48
40
(1)根据表中的数据判断p是V的________.(①一次函数;②反比例函数;③二次函数.填序号即可)
(2)确定p与V的函数关系式,并在如图所示的坐标系内画出该函数的大致图象;
(3)当气球内的气体压强大于140kPa时,气球将爆炸,为了安全起见,气体的体积V(m3)的取值范围是________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形网格中,△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
(1)作出△ABC关于原点O成中心对称的△A1B1C1;
(2)直接写出:以A、B、C为顶点的平形四边形的第四个顶点D的坐标 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①当x≥1时,y随x的增大而减小;②b+2a=0;③x=3是关于x的方程ax2+bx+c=0(a≠0)的一个根;④4a-2b+c<0.其中正确的是________(填序号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-6,0),B(-1,1),C(-3,3),将△ABC绕点B按顺时针方向旋转90°后得到△A1BC1.
(1)画出△A1BC1,写出点A1、C1的坐标;
(2)计算线段BA扫过的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形
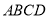 内有一点
内有一点 满足
满足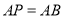 ,
, .连接
.连接 、
、 .
.
(1)求证:
 ;
;(2)求
 的度数.
的度数.
相关试题

