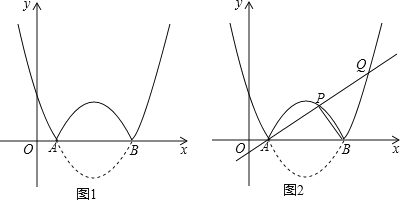
【题目】如图,抛物线l:y=![]() (x﹣h)2﹣2与x轴交于A,B两点(点A在点B的左侧),将抛物线ι在x轴下方部分沿轴翻折,x轴上方的图象保持不变,就组成了函数的图象.
(x﹣h)2﹣2与x轴交于A,B两点(点A在点B的左侧),将抛物线ι在x轴下方部分沿轴翻折,x轴上方的图象保持不变,就组成了函数的图象.
(1)若点A的坐标为(1,0).
①求抛物线l的表达式,并直接写出当x为何值时,函数的值y随x的增大而增大;
②如图2,若过A点的直线交函数的图象于另外两点P,Q,且S△ABQ=2S△ABP,求点P的坐标;
(2)当2<x<3时,若函数f的值随x的增大而增大,直接写出h的取值范围.
参考答案:
【答案】(1)①当1<x<3或x>5时,函数的值y随x的增大而增大,②P(![]() ,
,![]() );(2)当3≤h≤4或h≤0时,函数f的值随x的增大而增大.
);(2)当3≤h≤4或h≤0时,函数f的值随x的增大而增大.
【解析】
试题分析:(1)①利用待定系数法求抛物线的解析式,由对称性求点B的坐标,根据图象写出函数的值y随x的增大而增大(即呈上升趋势)的x的取值;
②如图2,作辅助线,构建对称点F和直角角三角形AQE,根据S△ABQ=2S△ABP,得QE=2PD,证明△PAD∽△QAE,则![]() ,得AE=2AD,设AD=a,根据QE=2FD列方程可求得a的值,并计算P的坐标;
,得AE=2AD,设AD=a,根据QE=2FD列方程可求得a的值,并计算P的坐标;
(2)先令y=0求抛物线与x轴的两个交点坐标,根据图象中呈上升趋势的部分,有两部分:分别讨论,并列不等式或不等式组可得h的取值.
试题解析:(1)①把A(1,0)代入抛物线y=![]() (x﹣h)2﹣2中得:
(x﹣h)2﹣2中得:
![]() (x﹣h)2﹣2=0,解得:h=3或h=﹣1,
(x﹣h)2﹣2=0,解得:h=3或h=﹣1,
∵点A在点B的左侧,∴h>0,∴h=3,
∴抛物线l的表达式为:y=![]() (x﹣3)2﹣2,
(x﹣3)2﹣2,
∴抛物线的对称轴是:直线x=3,
由对称性得:B(5,0),
由图象可知:当1<x<3或x>5时,函数的值y随x的增大而增大;
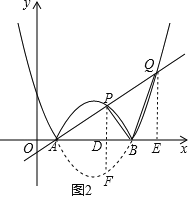
②如图2,作PD⊥x轴于点D,延长PD交抛物线l于点F,作QE⊥x轴于E,则PD∥QE,
由对称性得:DF=PD,
∵S△ABQ=2S△ABP,∴![]() ABQE=2×
ABQE=2×![]() ABPD,∴QE=2PD,
ABPD,∴QE=2PD,
∵PD∥QE,∴△PAD∽△QAE,∴![]() ,∴AE=2AD,
,∴AE=2AD,
设AD=a,则OD=1+a,OE=1+2a,P(1+a,﹣[![]() (1+a﹣3)2﹣2]),
(1+a﹣3)2﹣2]),
∵点F、Q在抛物线l上,
∴PD=DF=﹣[![]() (1+a﹣3)2﹣2],QE=
(1+a﹣3)2﹣2],QE=![]() (1+2a﹣3)2﹣2,
(1+2a﹣3)2﹣2,
∴![]() (1+2a﹣3)2﹣2=﹣2[
(1+2a﹣3)2﹣2=﹣2[![]() (1+a﹣3)2﹣2],
(1+a﹣3)2﹣2],
解得:a=![]() 或a=0(舍),∴P(
或a=0(舍),∴P(![]() ,
,![]() );
);
(2)当y=0时,![]() (x﹣h)2﹣2=0,
(x﹣h)2﹣2=0,
解得:x=h+2或h﹣2,
∵点A在点B的左侧,且h>0,∴A(h﹣2,0),B(h+2,0),
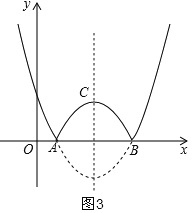
如图3,作抛物线的对称轴交抛物线于点C,
分两种情况:
①由图象可知:图象f在AC段时,函数f的值随x的增大而增大,
则![]() ,∴3≤h≤4,
,∴3≤h≤4,
②由图象可知:图象f点B的右侧时,函数f的值随x的增大而增大,
即:h+2≤2,h≤0,
综上所述,当3≤h≤4或h≤0时,函数f的值随x的增大而增大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中国倡导的“一带一路”建设将促进我国与世界各国的互利合作,根据规划,“一带一路”地区覆盖总人口约为4400000000人,这个数用科学记数法表示为( )
A.44×108B.4.4×109C.4.4×108D.4.4×1010
-
科目: 来源: 题型:
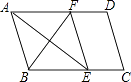
查看答案和解析>>【题目】如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为( )
A.13
B.14
C.15
D.16 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的一边中点M到对角线交点O的距离为5cm,则菱形ABCD的周长为( )
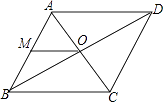
A.5cm
B.10cm
C.20cm
D.40cm -
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:a2b﹣4ab2+4b3=____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a2+a2=a4B.(a2)3=a5C.2a2﹣a2=2D.a5a2=a7
-
科目: 来源: 题型:
查看答案和解析>>【题目】七年级有x名男生,y名女生,则七年级共有名学生.
相关试题

