【题目】如图,抛物线![]() 经过
经过![]() 、
、![]() 两点,与
两点,与![]() 轴交于另一点
轴交于另一点![]() .
.
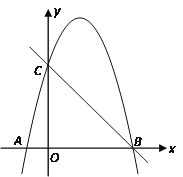
(1)求抛物线的解析式,并直接写出B点的坐标;
(2)已知点![]() 在第一象限的抛物线上,求点
在第一象限的抛物线上,求点![]() 关于直线
关于直线![]() 对称的点的坐标;
对称的点的坐标;
(3)在(2)的条件下,连接![]() ,点
,点![]() 为抛物线上一点,且
为抛物线上一点,且![]() ,求点
,求点![]() 的坐标.
的坐标.
参考答案:
【答案】(1)y=-x2+3x+4.B(4,0);(2)(0,1).(3)(2,6)
【解析】
试题分析:(1)将点A、C的坐标代入抛物线的解析式中,然后解方程组即可.然后令y=0,即可解决问题;
(2)首先由(1)的抛物线解析式确定点D的坐标,此时可以看出CD平行于x轴,由于OB=OC,即△OCB是等腰直角三角形,所以∠OCB=∠DCB=45°,因此点D关于直线BC的对称点恰好在y轴上,将点C向下平移CD长个单位就能求出这个对称点的坐标.
(3)利用待定系数法先求出直线BC的解析式,然后过点P作y轴的平行线,交直线BC于点Q,用未知数设出点P、Q的坐标,即可得到线段PQ的长度表达式,以PQ为底、OB为高,即可得到△PBC的面积函数关系式,根据函数的性质即可求出△PBC的面积最大时,点P的坐标.
试题解析:(1)依题意,有:
![]() ,解得
,解得![]()
∴抛物线的解析式:y=-x2+3x+4.
令y=0,则-x2+3x+4=0
解得:x1=-1,x2=4
故B(4,0);
(2)将点D(m,m+1)代入y=-x2+3x+4中,得:
-m2+3m+4=m+1,化简,得:m2-2m-3=0
解得:m1=-1(舍),m2=3;
∴D(3,4),因此CD∥x轴;
由B(4,0)、C(0,4)可得:OB=OC=4,即△OBC是等腰直角三角形,得:
∠OCB=∠DCB=45°;
设点D关于直线BC的对称点为点E,则点E在y轴上,且CD=CE=3,OE=OC-CE=1,则:
点D关于直线BC的对称点的坐标为(0,1).
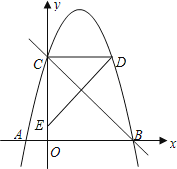
(3)由B(4,0)、C(0,4)可知,直线BC:y=-x+4;
过点P作PQ∥y轴,交直线BC于Q,
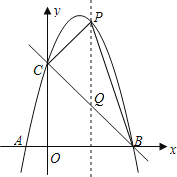
设P(x,-x2+3x+4),则Q(x,-x+4);
∴PQ=(-x2+3x+4)-(-x+4)=-x2+4x;
S△PCB=![]() PQ×OB=
PQ×OB=![]() ×(-x2+4x)×4=-2(x-2)2+8;
×(-x2+4x)×4=-2(x-2)2+8;
所以,当P(2,6)时,△PCB的面积最大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)2x3·x2-x11+(x2)3; (2)(x-5)(x+1)-(x-2)2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上的A点表示的数是-3,数轴上另一点B到A点的距离是2,则B点所表示的数是____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:x3﹣4xy2=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个命题中,真命题有( )
①两条直线被第三条直线所截,内错角相等.
②如果∠1和∠2是对顶角,那么∠1=∠2.
③三角形的一个外角大于任何一个内角.
④如果x2>0,那么x>0.
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在大课间活动中,体育老师对甲、乙两名同学每人进行10次立定跳远测试,他们的平均成绩相同,方差分别是S甲=0.20,S乙=0.16,则甲、乙两名同学成绩更稳定的是______.
-
科目: 来源: 题型:
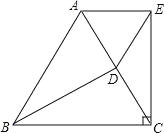
查看答案和解析>>【题目】如图,已知△ABC是等边三角形,D为边AC的中点,AE⊥EC,BD=EC.
(1)求证:△BDA≌△CEA;
(2)请判断△ADE是什么三角形,并说明理由.
相关试题

