【题目】已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).

(1)四边形EFGH是什么四边形?证明你的结论.
(2)当四边形ABCD的对角线满足 条件时,四边形EFGH是矩形;
(3)你学过的哪种特殊四边形的中点四边形是矩形? . (填一种即可)
参考答案:
【答案】(1)四边形EFGH的形状是平行四边形.理由见解析;(2)当四边形ABCD的对角线满足互相垂直的条件时,四边形EFGH是矩形.(3)矩形.
【解析】
试题解析:(1)连接BD,根据三角形的中位线定理得到EH∥BD,EH=![]() BD,FG∥BD,FG=
BD,FG∥BD,FG=![]() BD,推出,EH∥FG,EH=FG,根据一组对边平行且相等的四边形是平行四边形得出四边形EFGH是平行四边形;
BD,推出,EH∥FG,EH=FG,根据一组对边平行且相等的四边形是平行四边形得出四边形EFGH是平行四边形;
(2)根据有一个角是直角的平行四边形是矩形,可知当四边形ABCD的对角线满足AC⊥BD的条件时,四边形EFGH是矩形;
(3)菱形的中点四边形是矩形.根据三角形的中位线平行于第三边并且等于第三边的一半可得EH∥BD,EF∥AC,再根据矩形的每一个角都是直角可得∠1=90°,然后根据平行线的性质求出∠3=90°,再根据垂直定义解答.
试题解析:(1)四边形EFGH的形状是平行四边形.理由如下:
如图,连结BD.
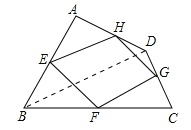
∵E、H分别是AB、AD中点,
∴EH∥BD,EH=![]() BD,
BD,
同理FG∥BD,FG=![]() BD,
BD,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形;
(2)当四边形ABCD的对角线满足互相垂直的条件时,四边形EFGH是矩形.理由如下:
如图,连结AC、BD.

∵E、F、G、H分别为四边形ABCD四条边上的中点,
∴EH∥BD,HG∥AC,
∵AC⊥BD,
∴EH⊥HG,
又∵四边形EFGH是平行四边形,
∴平行四边形EFGH是矩形;
(3)菱形的中点四边形是矩形.理由如下:
如图,连结AC、BD.
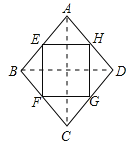
∵E、F、G、H分别为四边形ABCD四条边上的中点,
∴EH∥BD,HG∥AC,FG∥BD,EH=![]() BD,FG=
BD,FG=![]() BD,
BD,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形.
∵四边形ABCD是菱形,
∴AC⊥BD,
∵EH∥BD,HG∥AC,
∴EH⊥HG,
∴平行四边形EFGH是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角三角形ABC中,斜边AB=1,则AB+BC+AC=_____
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰梯形ABCD中,AD∥BC,AD=1,BC=3,AB=CD=2,点E在BC边上,AE与BD交于点F,∠BAE=∠DBC,
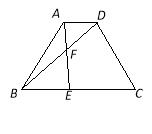
(1)求证:△ABE∽△BCD;
(2)求tan∠DBC的值;
(3)求线段BF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′.
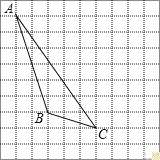
(1)补全△A′B′C′,利用网格点和直尺画图;
(2)图中AC与A1C1的关系是: ;
(3)画出AB边上的高线CD;
(4)画出△ABC中AB边上的中线CE;
(5)△BCE的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程为ax2+bx+5=0(a≠0)的解是x=1,则2013﹣a﹣b的值是( )
A.2 018
B.2 008
C.2 014
D.2 012 -
科目: 来源: 题型:
查看答案和解析>>【题目】化简﹣2(m﹣n)的结果为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列判断错误的是( )
A.两组对边分别相等的四边形是平行四边形
B.四个内角都相等的四边形是矩形
C.四条边都相等的四边形是菱形
D.两条对角线垂直且平分的四边形是正方形
相关试题

