【题目】九年级一班组织班级联欢会,最后进入抽奖环节,每名同学都有一次抽奖机会,抽奖方案如下:将一副扑克牌中点数为“2”,“3”,“3”,“5”,“6”的五张牌背面朝上洗匀,先从中抽出1张牌,再从余下的4张牌中抽出1张牌,记录两张 牌点数后放回,完成一次抽奖,记每次抽出两张牌点数之差为x,按表格要求确定奖项.
![]()
(1)用列表或画树状图的方法求出甲同学获得一等奖的概率;
(2)是否每次抽奖都会获奖,为什么?
参考答案:
【答案】(1)![]() ;(2)不一定.理由见解析.
;(2)不一定.理由见解析.
【解析】
试题分析:(1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与甲同学获得一等奖的情况,再利用概率公式即可求得答案;
(2)由树状图可得:当两张牌都是2时,|x|=0,不会有奖.
试题解析:(1)画树状图得:
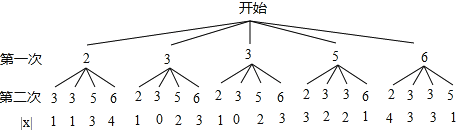
∵共有20种等可能的结果,甲同学获得一等奖的有2种情况,
∴甲同学获得一等奖的概率为:![]() ;
;
(2)不一定,当两张牌都是3时,|x|=0,不会有奖.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若|a+5|+(b﹣4)2=0,则(a+b)2009=__.
-
科目: 来源: 题型:
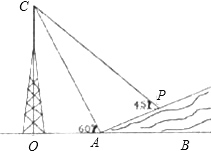
查看答案和解析>>【题目】如图某人在一斜坡坡脚A处测得电视塔塔尖C的仰角为60°,沿斜坡向上走到P处再测得塔尖C的仰角为45°,若OA=45米,斜坡的坡比(竖直高度与水平高度的比)为1:2,且O、A、B在同一条直线上.求电视塔OC的高度及此人所在位置P到AB的距离.(测角器高度忽略不计,结果精确到0.1米.参考数据:
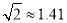 ,
,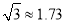 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】将两个全等的直角三角形ABC和DBE按图①方式摆放,其中∠ACB=∠DEB=90°,∠A=∠D=30°,点E落在AB上,DE所在直线交AC所在直线于点F。

(1)求证:AF+EF=DE;
(2)若将图①中的△DBE绕点B按顺时针方向旋转角α,且0°<α<60°,其它条件不变,请在图②中画出变换后的图形,并直接写出你在(1)中猜想的结论是否仍然成立;
(3)若将图①中的△DBE绕点B按顺时针方向旋转角β,且60°<β<180°,其它条件不变,如图③,你认为(1)中猜想的结论还成立吗?若成立,写出证明过程;若不成立,请写出AF、EF与DE之间的关系,并说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】将某图形的横坐标都减去2,纵坐标不变,则该图形( )
A. 向右平移2个单位
B. 向左平移2个单位
C. 向上平移2个单位
D. 向下平移2个单位
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列算式: 31=3,32=9,33=27,34=81,35=243,36=729,37=2187,38=6561,…,根据上述算式中的规律,你认为32015的末位数字是__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的顶角y与底角x之间是函数关系吗?(是或不是中选择)
相关试题

