【题目】如图,在等腰直角△ABC中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P,则下列结论:①图中全等的三角形只有两对;②△ABC的面积等于四边形CDOE面积的2倍;③OD=OE;④CE+CD=BC,其中正确的结论有( )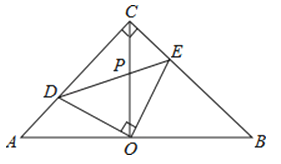
A.1个
B.2个
C.3个
D.4个
参考答案:
【答案】C
【解析】解:结论①错误.理由如下:
图中全等的三角形有3对,分别为△AOC≌△BOC,△AOD≌△COE,△COD≌△BOE.
由等腰直角三角形的性质,可知OA=OC=OB,易得△AOC≌△BOC.
∵OC⊥AB,OD⊥OE,
∴∠AOD=∠COE.
在△AOD与△COE中, ,
,
∴△AOD≌△COE(ASA).
同理可证:△COD≌△BOE.
结论②正确.理由如下:
∵△AOD≌△COE,
∴S△AOD=S△COE ,
∴S四边形CDOE=S△COD+S△COE=S△COD+S△AOD=S△AOC=![]() S△ABC ,
S△ABC ,
即△ABC的面积等于四边形CDOE的面积的2倍.
结论③正确,理由如下:∵△AOD≌△COE,
∴OD=OE;
结论④正确,理由如下:
∵△AOD≌△COE,
∴CE=AD,
∵AB=AC,
∴CD=EB,
∴CD+CE=EB+CE=BC.
综上所述,正确的结论有3个.
故选:C.
结论①错误.因为图中全等的三角形有3对;
结论②正确.由全等三角形的性质可以判断;
结论③正确.利用全等三角形的性质可以判断.
结论④正确.利用全等三角形和等腰直角三角形的性质可以判断.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.(x3)2=x5
B.(﹣x)5=﹣x5
C.x3x2=x6
D.3x2+2x3=5x5 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算结果正确的是( )
A. a3+a4=a7 B. a4÷a3=a C. a3a2=2a3 D. (a3)3=a6
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题:“P 是等边△ABC 内的一点,若 P 到三边的距离相等,则 PA=PB=PC.”
(1)写出它的逆命题.判断其逆命题成立吗?若成立,请给出证明.
(2)进一步证明:点 P 到等边△ABC 各边的距离之和为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a2a3=a6B.a6÷a2=a3C.(a2)3=a6D.a6﹣a2=a4
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,假命题有( )
①两点之间线段最短;②到角的两边距离相等的点在角的平分线上;
③过一点有且只有一条直线与已知直线平行;④垂直于同一直线的两条直线平行;
⑤若⊙
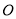 的弦
的弦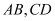 交于点
交于点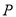 ,则
,则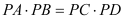 .
.A.4个 B.3个 C. 2个 D.1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图所示.A、B、C三点在格点上.

①作出△ABC关于x轴对称的△A1B1C1 , 并写出点C1的坐标;
②作出△ABC关于y对称的△A2B2C2 , 并写出点C2的坐标.
相关试题

