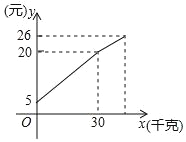
【题目】王大爷带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价出售一些后,又降价出售,售出土豆的千克数x与他手中持有的钱数y(含备用零钱)的关系如图所示.根据图象回答下列问题:
(1)王大爷自带的零钱是多少?
(2)降价前他每千克土豆出售的价格是多少?
(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克土豆?
(4)写出售出土豆的千克数x与他手中持有的钱数y(含备用零钱)的关系式.
参考答案:
【答案】(1)王大爷自带的零钱是5元;(2)降价前每千克的土豆价格是0.5元/千克;(3)一共带了45千克;(4) 降价前:y=![]() x+5;降价后:y=0.4x+8.
x+5;降价后:y=0.4x+8.
【解析】
(1)直接根据图象与y轴的交点可知:农民自带的零钱是5元;
(2)根据销售30千克收入的钱数是20﹣5=15元,据此即可求得降价前的价格;
(3)根据降价后销售的钱数是26﹣20=6元,单价是每千克0.4元,即可求得降价销售的数量,进而求得销售的总的数量;
(4)利用待定系数法即可求解.
(1)由图象可得:王大爷自带的零钱是5元;
(2)降价前每千克的土豆价格是:![]() 0.5(元/千克);
0.5(元/千克);
(3)(26﹣20)÷0.4=15(千克),则一共带了30+15=45(千克).
(4)设降价出售前,王大爷手中的钱数与售出的土豆千克数的关系为:y=kx+b,把点(0,5),(30,20)代入可得:![]() ,解得:
,解得: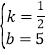 ,则函数解析式是:y
,则函数解析式是:y![]() x+5;
x+5;
设降价后的函数解析式是y=mx+n,根据题意得:![]() ,解得:
,解得:![]() ,则函数解析式是:y=0.4x+8.
,则函数解析式是:y=0.4x+8.
故降价前,函数解析式是:y=![]() x+5;降价后,函数解析式是:y=0.4x+8.
x+5;降价后,函数解析式是:y=0.4x+8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△AOD是等腰直角三角形,AB=AC,AO=AD,∠BAC=∠OAD=90°,点O是△ABC内的一点,∠BOC=130°.
(1)求证:OB=DC;
(2)求∠DCO的大小;
(3)设∠AOB=α,那么当α为多少度时,△COD是等腰三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下列证明过程.
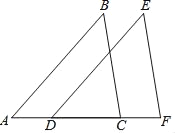
如图,已知AB∥DE,AB=DE,D,C在AF上,且AD=CF,求证:△ABC≌△DEF.
证明:∵AB∥DE
∴∠_____=∠_____(_______)
∵AD=CF
∴AD+DC=CF+DC即_____
在△ABC和△DEF中AB=DE_____
∴△ABC≌△DEF_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】按下面的方法折纸,然后回答问题:

(1)∠1与∠AEC有何关系?
(2)∠1,∠3有何关系?
(3)∠2是多少度的角?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明是个爱动脑筋的学生,在学习了解直角三角形以后,一天他去测量学校的旗杆DF的高度,此时过旗杆的顶点F的阳光刚好过身高DE为1.6米的小明的头顶且在他身后形成的影长DC=2米.
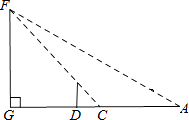
(1)若旗杆的高度FG是a米,用含a的代数式表示DG.
(2)小明从点C后退6米在A的测得旗杆顶点F的仰角为30°,求旗杆FG的高度.(点A、C、D、G在一条直线上,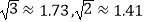 ,结果精确到0.1)
,结果精确到0.1) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在矩形ABCD中,AB=a,BC=b,点E是线段AD边上的任意一点(不含端点A、D),连结BE、CE.
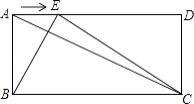
(1)若a=5,sin∠ACB=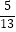 ,求b.
,求b.
(2)若a=5,b=10当BE⊥AC时,求出此时AE的长.
(3)设AE=x,试探索点E在线段AD上运动过程中,使得△ABE与△BCE相似时,求a、b应满足什么条件,并求出此时x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知下列方程:①
 ;②0.3x=1;③
;②0.3x=1;③ ;④x2﹣4x=3;⑤x=6;⑥x+2y=0.其中一元一次方程的个数是( )
;④x2﹣4x=3;⑤x=6;⑥x+2y=0.其中一元一次方程的个数是( )A. 2B. 3C. 4D. 5
相关试题

