【题目】已知等腰梯形ABCD中,AB∥CD,对角线AC、BD相交于O,∠ABD=30°,AC⊥BC,AB=8cm,则△COD的面积为( )
A.![]()
cm2
B.![]()
cm2
C.![]()
cm2
D.![]()
cm2
参考答案:
【答案】A
【解析】解:∵梯形ABCD是等腰梯形,CD∥AB,
由SAS可证△DAB≌△CBA,
∴∠CAB=∠DCA=30°,
∵∠CAB=30°,又因为AC⊥BC,
∴∠DAB=∠CBA=60°,
∴∠DAC=∠DCA=30°,
∴CD=AD=BC=4cm,
∴AC2=AB2﹣BC2 ,
∴AC=4 ![]() cm,
cm,
∵梯形ABCD是等腰梯形,
∴AC=BD=4 ![]() cm,
cm,
∴S△ABC= ![]() ×4×4
×4×4 ![]() =8
=8 ![]() cm2 ,
cm2 ,
设DO为x,则CO=x,则AO=BO=(4 ![]() ﹣x)cm,
﹣x)cm,
在Rt△COB中,CO2+BC2=BO2 ,
即:x2+42=(4 ![]() ﹣x)2
﹣x)2
∴D0= ![]() cm,
cm,
∴S△ADO= ![]() ×
× ![]() ×4=
×4= ![]() ,
,
∴S△AOB=S△ABC﹣S△ADO= ![]()
∵AB∥CD,
∴△AOB∽△DOC,
∴( ![]() )2=
)2= ![]()
∴S△DOC= ![]() ,
,
故选:A.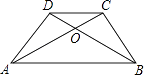
【考点精析】掌握等腰梯形的性质是解答本题的根本,需要知道等腰梯形的两腰相等;同一底上的两个角相等;两条对角线相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】周末,身高都为1.6米的小芳、小丽来到溪江公园,准备用她们所学的知识测算南塔的高度.如图,小芳站在A处测得她看塔顶的仰角α为45°,小丽站在B处(A、B与塔的轴心共线)测得她看塔顶的仰角β为30°.她们又测出A、B两点的距离为30米.假设她们的
眼睛离头顶都为10cm,则可计算出塔高约为(结果精确到0.01,参考数据: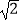 ≈1.414,
≈1.414, 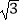 ≈1.732)( )
≈1.732)( )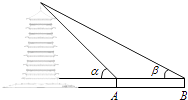
A.36.21米
B.37.71米
C.40.98米
D.42.48米 -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店购买60件A商品和30件B商品共用了1080元,购买50件A商品和20件B商品共用了880元.
(1)A、B两种商品的单价分别是多少元?
(2)已知该商店购买B商品的件数比购买A商品的件数的2倍少4件,如果需要购买A、B两种商品的总件数不少于32件,且该商店购买的A、B两种商品的总费用不超过296元,那么该商店有哪几种购买方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(2018﹣π)0=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公园的门票价格如下表所示:

某校九年级甲、乙两个班共100多人去该公园举行毕业联欢活动,其中甲班有50多人,乙班不足50人,如果以班为单位分别买门票,两个班一共应付920元;如果两个班联合起来作为一个团体购票,一共要付515元,问甲、乙两班分别有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是边长为a的正方形ABCD的中心,将一块半径足够长、圆心为直角的扇形纸板的圆心放在O点处,并将纸板的圆心绕O旋转,则正方形ABCD被纸板覆盖部分的面积为( )

A.
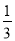 a2 B.
a2 B. 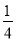 a2 C.
a2 C. 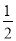 a2 D.
a2 D. 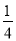 a
a -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,我们把横、纵坐标都是整数的点叫做整点,且规定:正方形内部 不包含边界上的点.观察如图所示的中心在原点、一边平行于 x 轴的正方形:边长为 1 的正方形内部有 1 个整点,边长为 2 的正方形内部有 1 个整点,边长为 3 的正方形内部 有 9 个整点,…,则边长为 10 的正方形内的整点个数为( )

A. 64 个 B. 100 个 C. 81 个 D. 121 个
相关试题

