【题目】设函数f(x)=|x+ ![]() |+|x﹣2m|(m>0). (Ⅰ)求证:f(x)≥8恒成立;
|+|x﹣2m|(m>0). (Ⅰ)求证:f(x)≥8恒成立;
(Ⅱ)求使得不等式f(1)>10成立的实数m的取值范围.
参考答案:
【答案】解:(Ⅰ)证明:函数f(x)=|x+ ![]() |+|x﹣2m|(m>0), ∴f(x)=|x+
|+|x﹣2m|(m>0), ∴f(x)=|x+ ![]() |+|x﹣2m|≥|x+
|+|x﹣2m|≥|x+ ![]() ﹣(x﹣2m)|=|
﹣(x﹣2m)|=| ![]() +2m|=
+2m|= ![]() +2m≥2
+2m≥2 ![]() =8,
=8,
当且仅当m=2时,取等号,故f(x)≥8恒成立.
(Ⅱ)f(1)=|1+ ![]() |+|1﹣2m|,当m>
|+|1﹣2m|,当m> ![]() 时,f(1)=1+
时,f(1)=1+ ![]() ﹣(1﹣2m),不等式即
﹣(1﹣2m),不等式即 ![]() +2m>10,
+2m>10,
化简为m2﹣5m+4>0,求得m<1,或m>4,故此时m的范围为( ![]() ,1)∪(4,+∞).
,1)∪(4,+∞).
当0<m≤ ![]() 时,f(1)=1+
时,f(1)=1+ ![]() +(1﹣2m)=2+
+(1﹣2m)=2+ ![]() ﹣2m关于变量m单调递减,
﹣2m关于变量m单调递减,
故当m= ![]() 时,f(1)取得最小值为17,
时,f(1)取得最小值为17,
故不等式f(1)>10恒成立.
综上可得,m的范围为(0,1)∪(4,+∞)
【解析】(Ⅰ)利用绝对值三角不等式、基本不等式证得f(x)≥8恒成立.(Ⅱ)当m> ![]() 时,不等式即
时,不等式即 ![]() +2m>10,即m2﹣5m+4>0,求得m的范围.当0<m≤
+2m>10,即m2﹣5m+4>0,求得m的范围.当0<m≤ ![]() 时,f(1)=1+
时,f(1)=1+ ![]() +(1﹣2m)=2+
+(1﹣2m)=2+ ![]() ﹣2m关于变量m单调递减,求得f(1)的最小值为17,可得不等式f(1)>10恒成立.综合可得m的范围.
﹣2m关于变量m单调递减,求得f(1)的最小值为17,可得不等式f(1)>10恒成立.综合可得m的范围.
【考点精析】本题主要考查了绝对值不等式的解法的相关知识点,需要掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线x2=2py(p>0)的焦点为F,直线x=4与x轴的交点为P,与抛物线的交点为Q,且
 .
.
(1)求抛物线的方程;
(2)如图所示,过F的直线l与抛物线相交于A,D两点,与圆x2+(y﹣1)2=1相交于B,C两点(A,B两点相邻),过A,D两点分别作我校的切线,两条切线相交于点M,求△ABM与△CDM的面积之积的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=axln(x+1)+x+1(x>﹣1,a∈R).
(1)若 ,求函数f(x)的单调区间;
,求函数f(x)的单调区间;
(2)当x≥0时,不等式f(x)≤ex恒成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线C1的参数方程为
 (t为参数),以原点O为极点,以x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为
(t为参数),以原点O为极点,以x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为  . (I)求曲线C2的直角坐标系方程;
. (I)求曲线C2的直角坐标系方程;
(II)设M1是曲线C1上的点,M2是曲线C2上的点,求|M1M2|的最小值. -
科目: 来源: 题型:
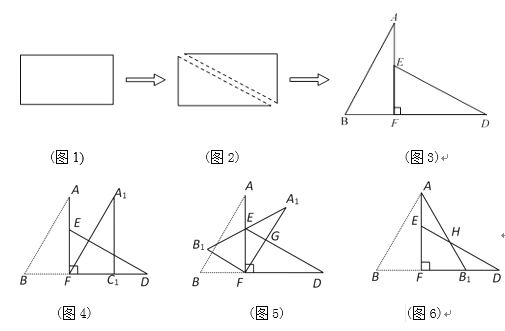
查看答案和解析>>【题目】如图1,小明将一张矩形纸片沿对角线剪开,得到两张三角形纸片(如图2),量得他们的斜边长为10cm,较短直角边长为5cm,较小锐角为30°,再将这两张三角纸片摆成如图3的形状,但点B、C、F、D在同一条直线上,且点C与点F重合(在图3至图6中统一用F表示),小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决.
(1)将图3中的△ABF沿BD向右平移到图4的位置,使点B与点F 重合,请你求出平移的距离;
(2)将图3中的△ABF绕点F顺时针方向旋转30°到图5的位置,A1F交DE于点G,请你求出线段FG的长度;
(3)将图3中的△ABF沿直线AF翻折到图6的位置,AB1交DE于点H,请证明:AH=DH
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义在R上的奇函数f(x)满足f(x+1)=f(﹣x),当x∈(0,
 ]时,f(x)=
]时,f(x)=  (1﹣x),则f(x)在区间(1,
(1﹣x),则f(x)在区间(1,  )内是( )
)内是( )
A.减函数且f(x)>0
B.减函数且f(x)<0
C.增函数且f(x)>0
D.增函数且f(x)<0 -
科目: 来源: 题型:
查看答案和解析>>【题目】执行右面的程序框图,如果输出的a值大于2017,那么判断框内的条件为( )

A.k<9?
B.k≥9?
C.k<10?
D.k≥11?
相关试题

