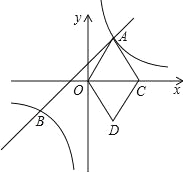
【题目】如图,在平面直角坐标系xOy中,直线y=mx+1与双曲y=![]() (k>0)相交于点A、B,点C在x轴正半轴上,点D(1,﹣2),连结OA、OD、DC、AC,四边形AODC为菱形.
(k>0)相交于点A、B,点C在x轴正半轴上,点D(1,﹣2),连结OA、OD、DC、AC,四边形AODC为菱形.
(1)求k和m的值;
(2)根据图象写出反比例函数的值小于2时x的取值范围;
(3)设点P是y轴上一动点,且![]() ,求点P的坐标.
,求点P的坐标.
参考答案:
【答案】(1)m=1;k=2;(2)x<0或x>1;;(3)(0,8)或(0,﹣8).
【解析】
试题分析:(1)由菱形的性质可知A、D关于x轴对称,可求得A点坐标,把A点坐标分别代入两函数函数解析式可求得k和m值;
(2)由(1)可知A点坐标为(1,2),结合图象可知在A点的下方时,反比例函数的值小于2,可求得x的取值范围;
(3)根据菱形的性质可求得C点坐标,可求得菱形面积,设P点坐标为(0,y),根据条件可得到关于y的方程,可求得P点坐标.
试题解析:(1)如图,连接AD,交x轴于点E,
∵D(1,2),
∴OE=1,ED=2,
∵四边形AODC是菱形,
∴AE=DE=2,EC=OE=1,
∴A(1,2),
将A(1,2)代入直线y=mx+1可得m+1=2,解得m=1,
将A(1,2)代入反比例函数y=![]() ,可求得k=2;
,可求得k=2;

(2)∵当x=1时,反比例函数的值为2,
∴当反比例函数图象在A点下方时,对应的函数值小于2,
此时x的取值范围为:x<0或x>1;
(3)∵OC=2OE=2,AD=2DE=4,
∴![]() =
=![]() OCAD=4,
OCAD=4,
∵![]() ,
,
∴![]() =4,
=4,
设P点坐标为(0,y),则OP=|y|,
∴![]() ×|y|×1=4,即|y|=8,
×|y|×1=4,即|y|=8,
解得y=8或y=﹣8,
∴P点坐标为(0,8)或(0,﹣8).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果线段AB=10cm,AC+BC=20cm,则下列说法正确的是( )
A. 点C在线段AB上 B. 点C不能在直线AB上
C. 点C只能在直线AB上 D. 点C可能在直线AB上,也可能在直线AB外
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OM是∠AOC的平分线,ON是∠BOC的平分线.

(1)如图1,当∠AOB=90°,∠BOC=60°时,∠MON的度数是多少?为什么?
(2)如图2,当∠AOB=70°,∠BOC=60°时,∠MON= (直接写出结果)
(3)如图3,当∠AOB=α,∠BOC=β时,猜想:∠MON= (直接写出结果). -
科目: 来源: 题型:
查看答案和解析>>【题目】在数学实验课上,李静同学剪了两张直角三角形纸片,进行如下的操作:
操作一:如图1,将Rt△ABC纸片沿某条直线折叠,使斜边两个端点A与B重合,折痕为DE.
(1)如果AC=5cm,BC=7cm,可得△ACD的周长为 ;
(2)如果∠CAD:∠BAD=1:2,可得∠B的度数为 ;
操作二:如图2,李静拿出另一张Rt△ABC纸片,将直角边AC沿直线CD折叠,使点A与点E重合,若AB=10cm,BC=8cm,请求出BE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是用4个相同的小矩形与1个小正方形密铺而成的正方形图案,已知大正方形的面积为49,小正方形的面积为4,若用x,y(其中x>y)表示小矩形的长与宽,请观察图案,指出以下关系式中不正确的是( )
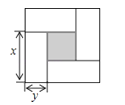
A.x+y=7
B.x﹣y=2
C.x2﹣y2=4
D.4xy+4=49 -
科目: 来源: 题型:
查看答案和解析>>【题目】小明的身高h超过了160cm,用不等式可表示为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上的点A到原点的距离是5,则点A所表示的数为( )
A. 5 B. ﹣5 C. 2.5 D. 5或﹣5
相关试题

