【题目】如图，已知抛物线经过点A(-3，0)，C(0，3)，交x轴于另一点B，其顶点为D．

（1）求抛物线的解析式；

（2）点P为抛物线上一点，直线CP交x轴于点E，若△CAE与△OCD相似，求P点坐标；

（3）如果点F在y轴上，点M在直线AC上，那么在抛物线上是否存在点N，使得以C，F，M，N为顶点的四边形是菱形？若存在，请求出菱形的周长；若不存在，请说明理由．

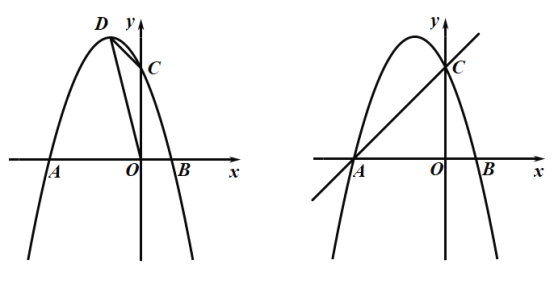
【答案】（1）；（2）P或；（3）存在菱形，其周长为，或．

【解析】

（1）将A，C两点坐标代入中求出b，c即可得解；

（2）根据题意进行分类讨论，两种情况，，从而求出E点坐标及CE解析式即可求出点P坐标；

（3）根据题意，分类讨论，两种情况CF为对角线，CF为菱形的一边，进而即可求得菱形的周长.

（1）∵抛物线经过点，

∴，解得

此抛物线解析式为：；

（2）∵

∴顶点

∵，，

∴，，，

∴点E只能在A点左边

①如下图，若

则

∴

∴

∴

∵

∴

联立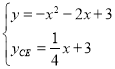

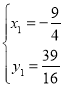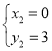∴，（舍去）

∴；

②若

则

∴AE=2

∴

∴

∵

∴

联立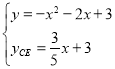

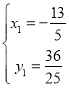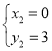∴，（舍去）

得

因此，或；

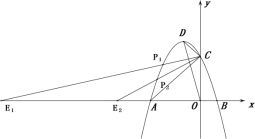
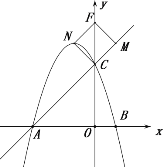
（3）在抛物线上存在点N，使得以C，F，M，N为顶点的四边形是菱形

①若CF为对角线，则CF与NM互相垂直平分时，四边形CNFM为菱形

∵

∴

∴，四边形CNFM为正方形

∴N点与顶点D重合

∵

∴，

∴菱形CNFM的周长为；

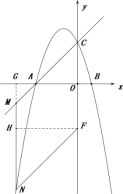
②若CF为菱形的一边，则，，NM=NF时，四边形CNFM为菱形

过F作FH⊥NM于H，设直线NM交x轴于G，

则,

∴NM===NF

∵，

∴

∴NF=FH

又FH=OG=

∴=

∴ 或

∴NF=或NF=菱形周长为或

因此，存在菱形，其周长为，或.

关闭