【题目】如图,点M,N分别是正五边形ABCDE的边BC,CD上的点,且BM=CN,AM交BN于点P.

(1)求证:△ABM≌△BCN;
(2)求∠APN的度数.
参考答案:
【答案】(1)由SAS可证(2)108°
【解析】试题分析:(1)利用正五边形的性质得出AB=BC,∠ABM=∠C,再利用全SAS即可判定△ABM≌△BCN;(2)利用全等三角形的性质得出∠BAM+∠ABP=∠APN,进而得出∠CBN+∠ABP=∠APN=∠ABC即可得出答案.
试题解析:解:(1)证明:∵正五边形ABCDE,
∴AB=BC,∠ABM=∠C,
∴在△ABM和△BCN中
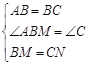 ,
,
∴△ABM≌△BCN(SAS);
(2)解:∵△ABM≌△BCN,
∴∠BAM=∠CBN,
∵∠BAM+∠ABP=∠APN,
∴∠CBN+∠ABP=∠APN=∠ABC=![]() .
.
即∠APN的度数为108°
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=6x2先向左平移2个单位,再向上平移3个单位后得到新的抛物线,则新抛物线解析式是( )
A.y=6(x﹣2)2+3
B.y=6(x+2)2+3
C.y=6(x﹣2)2﹣3
D.y=6(x+2)2﹣3 -
科目: 来源: 题型:
查看答案和解析>>【题目】关于等腰三角形和等边三角形的区别与联系,下列说法中,错误的是( )
A. 有一个角是60的等腰三角形是等边三角形
B. 等边三角形是等腰三角形的特殊情况
C. 等边三角形的底角与顶角相等
D. 等边三角形包括等腰三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋子中装有4个白球和3个黑球,它们除了颜色外都相同,随机从中摸出2个球,属于不可能事件的是( )
A.摸到2个白球
B.摸到2个黑球
C.摸到1个白球,1个黑球
D.摸到1个黑球,1个红球 -
科目: 来源: 题型:
查看答案和解析>>【题目】王大爷开了一个报亭,为了使每天进的某种报纸适量,王大爷对这种报纸40天的销售情况作了调查,这40天卖出这种报纸的份数如下:136、175、153、135、161、140、155、180、179、166、188、142、144、154、155、157、160、162、135、156、148、173、154、145、158、150、154、168、168、155、169、157、157、149、134、167、151、144、155、131.
将上面数据适当分组,作出频数直方图,说明王大爷每天进多少这种报纸比较合适?
-
科目: 来源: 题型:
查看答案和解析>>【题目】请写出一个开口向上,并且与y轴交于点(0,﹣1)的抛物线的解析式 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】两条直线相交成直角,就叫做两条直线互相垂直.这个句子是_____(填“定义”或“命题”).
相关试题

