【题目】根据《中华人民共和国个人所得税法》,新个税标准将于2019年1月1日起施行.其中每月纳税的起征点增加到5000元,即2019年1月以后每月工资中的5000元将不必缴纳税款.根据相关政策,纳税部门给大家制作了如下纳税表格(未完整):
级数 | 全月应纳税所得额(含税级距) | 税率( | 速算扣除数 |
1 | 不超过3000元的部分 |
| 0 |
2 | 超过3000元至12000元的部分 |
| 210 |
3 | 超过12000元至25000元的部分 |
| 1410 |
4 | 超过25000元至35000元的部分 |
|
|
5 | 超过35000元至55000元的部分 |
| 4410 |
6 | 超过55000元至80000元的部分 |
| 7160 |
7 | 超过80000元的部分 |
| 15160 |
例如:张三2019年1月如果月收入为21000元,则他1月中的![]() 元应该纳税,纳税数额为:
元应该纳税,纳税数额为:![]() (元).
(元).
(1)如果李士业2019年1月份收入为7000元,则他1月份应纳税多少元?
(2)如果王努利2019年1月份收入为10000元,则他月份应纳税多少元?
(3)钱勒凤跟朋友说,估计自己1月份应纳税3400元,则钱勤奋1月份收入约有多少元?
(4)根据表中各数据关系,求表格中的![]() ,
,![]() 的值.
的值.
参考答案:
【答案】(1)60元;(2)290元;(3)20950元;(4)![]() ,
,![]()
【解析】
(1)总收入减去5000算出应纳税所得额是2000,没有超过3000元,乘以3%即为纳税额;
(2)总收入减去5000算出应纳税所得额为5000,分为两个部分前3000元税率为3%,后2000元税率为10%,再把两个部分税额相加即为答案;
(3)设1月份收入为x元,由税额超过了3000×3%+9000×10%=990元,故应纳税所得额超过了12000元,故分为三个部分计算税额,即3000×3%+9000×10%+(x500030009000)×20%=3400,解方程杰克求出总收入;
(4)由数据得出速算扣除额=上一级最高应纳税所得额×(本级税率上级税率)+上一级速算扣除数,即可求出m和n的值.
解:(1)![]() 元;
元;
∴1月份纳税60元;
(2)![]() 元,
元,
∴应纳税290元;
(3)设1月份收入为![]() 元,依题意得,
元,依题意得,
![]()
解得,![]() .
.
∴1月收入约有29050元.
(4)由数据关系可知,![]() ;
;
依题意得,![]()
解得,![]() .
.
∴![]() ,
,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如下表:
原进价
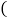 元
元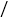 张
张
零售价
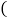 元
元 张
张
餐桌
a
270
餐椅
b
70
若购进4张餐桌19张餐椅需要1360元;若购进6张餐桌26张餐椅需要1940元.
 求表中a,b的值;
求表中a,b的值; 今年年初由于原材料价格上涨,每张餐桌的进价上涨了10元,每张餐椅的进价上涨了
今年年初由于原材料价格上涨,每张餐桌的进价上涨了10元,每张餐椅的进价上涨了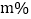 ,商场决定购进餐桌30张,餐椅170张进行销售,全部售出后,要求利润不低于7380元,求m的最大值.
,商场决定购进餐桌30张,餐椅170张进行销售,全部售出后,要求利润不低于7380元,求m的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+b2﹣4ac与反比例函数y=
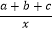 在同一坐标系内的图象大致为( )
在同一坐标系内的图象大致为( ) 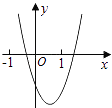
A.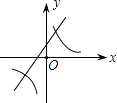
B.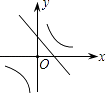
C.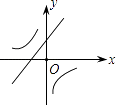
D.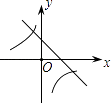
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料,解决下列问题:
材料一:对非负实数x“四舍五入”到个位的值记为
 ,即:当n为非负整数时,如果
,即:当n为非负整数时,如果 ,则
,则 ;反之,当n为非负整数时,如果
;反之,当n为非负整数时,如果 ;则
;则 ,例如:
,例如: ,
, ,
, ,
,
材料二:平面直角坐标系中任意两点
 ,
, ,我们把
,我们把 叫做
叫做 、
、 两点间的折线距离,并规定
两点间的折线距离,并规定 若
若 是一定点,
是一定点, 是直线
是直线 上的一动点,我们把
上的一动点,我们把 的最小值叫做
的最小值叫做 到直线
到直线 的折线距离,例如:若
的折线距离,例如:若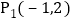 ,
, 则
则 .
. 如果
如果 ,写出实数x的取值范围;
,写出实数x的取值范围; 已知点
已知点 ,点
,点 ,且
,且 ,求a的值.
,求a的值. 若m为满足
若m为满足 的最大值,求点
的最大值,求点 到直线
到直线 的折线距离.
的折线距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】下面是二元一次方程组的不同解法,请你把下列消元的过程填写完整:
对于二元一次方程组

(1)方法一:由
 ,得
,得 
把
 代入
代入  ,得________________.
,得________________.(2)方法二:
 ,得
,得
 ,得________________.
,得________________.(3)方法三:
 ,得
,得 
 ,得________________.
,得________________.(4)方法四:由
 ,得
,得  ⑥
⑥把
 代入⑥,得________________.
代入⑥,得________________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,直线AB与y轴交于点
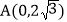 ,与x轴交于点B,
,与x轴交于点B,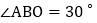 ,直线CD与y轴交于点D,与x轴交于点
,直线CD与y轴交于点D,与x轴交于点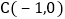 ,
,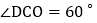 ,直线AB与直线CD交于点Q,E为直线CD上一动点,过点E作x轴的垂线,交直线AB于点M,交x轴于点N,连接AE、BE.
,直线AB与直线CD交于点Q,E为直线CD上一动点,过点E作x轴的垂线,交直线AB于点M,交x轴于点N,连接AE、BE. 求直线AB、CD的解析式及点Q的坐标;
求直线AB、CD的解析式及点Q的坐标; 当E点运动到Q点的右侧,且
当E点运动到Q点的右侧,且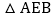 的面积为
的面积为 时,在y轴上有一动点P,直线AB上有一动点R,当
时,在y轴上有一动点P,直线AB上有一动点R,当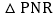 的周长最小时,求点P的坐标及
的周长最小时,求点P的坐标及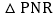 周长的最小值.
周长的最小值. 在
在 问的条件下,如图2将
问的条件下,如图2将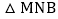 绕着点B逆时针旋转
绕着点B逆时针旋转 得到
得到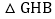 ,使点M与点G重合,点N与点H重合,再将
,使点M与点G重合,点N与点H重合,再将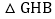 沿着直线AB平移,记平移中的
沿着直线AB平移,记平移中的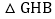 为
为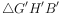 ,在平移过程中,设直线
,在平移过程中,设直线 与x轴交于点F,是否存在这样的点F,使得
与x轴交于点F,是否存在这样的点F,使得 为等腰三角形?若存在,求出此时点F的坐标;若不存在,说明理由
为等腰三角形?若存在,求出此时点F的坐标;若不存在,说明理由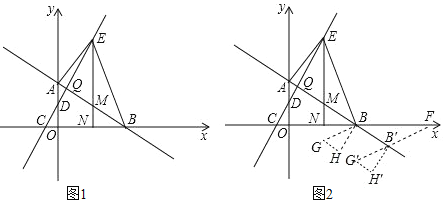
-
科目: 来源: 题型:
查看答案和解析>>【题目】商场正在销售帐篷和棉被两种防寒商品,已知购买
 顶帐篷和
顶帐篷和  床棉被共需
床棉被共需  元,购买
元,购买  顶帐篷和
顶帐篷和  床棉被共需
床棉被共需  元.
元.(1)求
 顶帐篷和
顶帐篷和  床棉被的价格各是多少元?
床棉被的价格各是多少元?(2)某学校准备购买这两种防寒商品共
 件,送给青海玉树灾区,要求每种商品都要购买,且帐篷的数量多于棉被的数量,但因为学校资金不足,购买总金额不能超过
件,送给青海玉树灾区,要求每种商品都要购买,且帐篷的数量多于棉被的数量,但因为学校资金不足,购买总金额不能超过  元,请问学校共有几种购买方案?(要求写出具体的购买方案)
元,请问学校共有几种购买方案?(要求写出具体的购买方案)
相关试题

