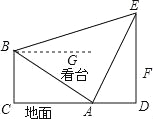
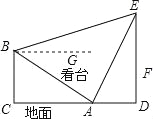
【题目】如图所示,体育场内一看台与地面所成夹角为30°,看台最低点A到最高点B的距离为10![]() ,A,B两点正前方有垂直于地面的旗杆DE.在A,B两点处用仪器测量旗杆顶端E的仰角分别为60°和15°(仰角即视线与水平线的夹角)
,A,B两点正前方有垂直于地面的旗杆DE.在A,B两点处用仪器测量旗杆顶端E的仰角分别为60°和15°(仰角即视线与水平线的夹角)
(1)求AE的长;
(2)已知旗杆上有一面旗在离地1米的F点处,这面旗以0.5米/秒的速度匀速上升,求这面旗到达旗杆顶端需要多少秒?
参考答案:
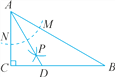
【答案】(1)AE的长为10![]() 米.
米.
(2)旗子到达旗杆顶端需要28秒.
【解析】
试题分析:(1)先求得∠ABE和AEB,利用等腰直角三角形即可求得AE;
(2)在RT△ADE中,利用sin∠EAD=![]() ,求得ED的长,即可求得这面旗到达旗杆顶端需要的时间.
,求得ED的长,即可求得这面旗到达旗杆顶端需要的时间.
试题解析:(1)∵BG∥CD,
∴∠GBA=∠BAC=30°,
又∵∠GBE=15°,
∴∠ABE=45°,
∵∠EAD=60°,
∴∠BAE=90°,
∴∠AEB=45°,
∴AB=AE=10![]() ,
,
故AE的长为10![]() 米.
米.
(2)在RT△ADE中,sin∠EAD=![]() ,
,
∴DE=10![]() ×
×![]() =15,
=15,
又∵DF=1,
∴FE=14,
∴时间t=![]() =28(秒).
=28(秒).
故旗子到达旗杆顶端需要28秒.
-
科目: 来源: 题型:
查看答案和解析>>【题目】宁波奥林匹克体育中心坐落于江北区,一期“三馆一圆”总投资35亿元,其中35亿元用科学记数法表示为( )
A.0.35×1010元
B.3.5×108元
C.3.5×109元
D.35×108元 -
科目: 来源: 题型:
查看答案和解析>>【题目】50个有理数相乘的积为0,那么( )
A.每一个因数都是0
B.每一个因数都不为0
C.最多有一个因数不为0
D.至少有一个因数为0 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧,分别交AB,AC于点M和N,再分别以点M,N为圆心,大于
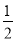 MN长为半径画弧,两弧交于点P,连结AP并延长,交BC于点D,则下列说法中,正确的个数是( )
MN长为半径画弧,两弧交于点P,连结AP并延长,交BC于点D,则下列说法中,正确的个数是( )①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC∶S△ABC=1∶3.
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】动手操作,探究:
探究一:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图(1),在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
探究二:若将△ADC改为任意四边形ABCD呢?
已知:如图(2),在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.(写出说理过程)
探究三:若将上题中的四边形ABCD改为六边形ABCDEF(图(3))呢?请直接写出∠P与∠A+∠B+∠E+∠F的数量关系.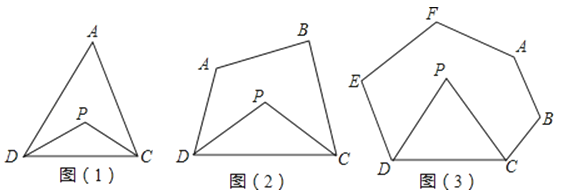
-
科目: 来源: 题型:
查看答案和解析>>【题目】若线段AB平行于x轴,AB长为5,若A的坐标为(4,5),则B的坐标为_________.
-
科目: 来源: 题型:
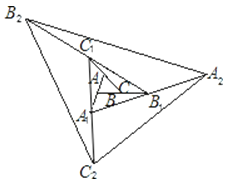
查看答案和解析>>【题目】如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1 , B1 , C1 , 使A1B=AB,B1C=BC,C1A=CA,顺次连接A1 , B1 , C1 , 得到△A1B1C1 . 第二次操作:分别延长A1B1 , B1C1 , C1A1至点A2 , B2 , C2 , 使A2B1=A1B1 , B2C1=B1C1 , C2A1=C1A1 , 顺次连接A2 , B2 , C2 , 得到△A2B2C2 , …按此规律,要使得到的三角形的面积超过2010,最少经过( )次操作.
A.6
B.5
C.4
D.3
相关试题

