【题目】(1)如图,一个直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY,XZ分别经过点B,C,△ABC中,若∠A=30°,则∠ABC+∠ACB=__ __,∠XBC+∠XCB=__ __;
(2)若改变直角三角板XYZ的位置,但三角板XYZ的两条直角边XY,XZ仍然分别经过点B,C,那么∠ABX+∠ACX的大小是否变化?若变化,请说明理由;若不变化,请求出∠ABX+∠ACX的大小.

参考答案:
【答案】(1)∠ABC+∠ACB=150°;(2分)∠XBC+∠XCB=90°.(2分)(2)∠XBC+∠XCB= 90°-X .(2分)
【解析】
(1)在△ABC中,利用三角形内角和等于180°,可求∠ABC+∠ACB=180°-∠A,即可求∠ABC+∠ACB;根据∠ABC+∠ACB=150°,∠XBC+∠XCB=90°,即可求出答案;
(2)不发生变化,由于在△ABC中,∠A=40°,从而∠ABC+∠ACB是一个定值,即等于140°,同理在△XBC中,∠BXC=90°,那么∠XBC+∠XCB也是一个定值,等于90°,于是∠ABX+∠ACX的值不变,等于140°-90°=50°.
(1)∵∠A=30°,
∴∠ABC+∠ACB=150°,
∵∠X=90°,
∴∠XBC+∠XCB=90°,
∴∠ABC+∠ACB=150°;
∵在△BCX中,∠BXC=90°,
∴∠XBC+∠XCB=90°,
∴∠ABX+∠ACX=140°-90°=50°;
故答案为:150°,90°;
(2)没有变化.
∵∠A=30°,
∴∠ABC+∠ACB=150°,
∵∠X=90°,
∴∠XBC+∠XCB=90°,
∴∠ABX+∠ACX=(∠ABC-∠XBC)+(∠ACB-∠XCB)=(∠ABC+∠ACB)-(∠XBC+∠XCB)=150°-90°=60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少? -
科目: 来源: 题型:
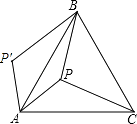
查看答案和解析>>【题目】如图,P是正三角形ABC内的一点,且PA=5,PB=12,PC=13,若将△PAC绕点A逆时针旋转后,得到△P′AB,求点P与点P′之间的距离及∠APB的度数.
-
科目: 来源: 题型:
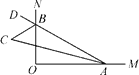
查看答案和解析>>【题目】如图,∠MON=90°,点A,B分别在射线OM,ON上移动,∠OAB的平分线与∠OBA的外角平分线交于点C,试猜想:随着点A,B的移动,∠ACB的大小是否发生变化,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣3,0)两点.
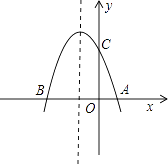
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;
(3)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若没有,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在同一直角坐标系中,函数y=mx+m和y=﹣mx2+2x+2(m是常数,且m≠0)的图象可能是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面内的两条直线有相交和平行两种位置关系.
(1)如图①,若AB∥CD,点P在AB,CD外部,则有 ∠B=∠BOD,又因为∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B-∠D.将点P移到AB,CD内部,如图②,以上结论是否成立?若成立,请说明理由;若不成立,则∠BPD,∠B,∠D之间有何数量关系?请证明你的结论;
(2)在图②中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图③,则∠BPD,∠B,∠D,∠BQD之间有何数量关系?(不需证明)
(3)根据(2)的结论,求图④中∠A+∠B+∠C+∠D+∠E的度数.

相关试题

