【题目】在△ABC中,∠A=55°,∠B 比∠C大25° ,则∠B 等于( )
A. 50° B. 100° C. 75° D. 125°
参考答案:
【答案】C
【解析】∵∠B比∠C大25°,
∴设∠B=x,则∠C=x-25°,
∵∠A+∠B+∠C=180°,∠A=55°,
∴55°+x+x-25°=180°,
解得x=75°,
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:a(3a+4b).
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一元二次方程ax2﹣bx﹣2019=0有一个根为x=﹣1,则a+b=_____.
-
科目: 来源: 题型:
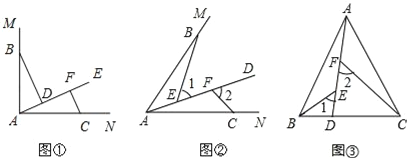
查看答案和解析>>【题目】(1)如图1,∠MAN=90°,射线AE在这个角的内部,点B、C分别在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.求证:△ABD≌△CAF;
(2)如图2,点B、C分别在∠MAN的边AM、AN上,点E、F都在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,且∠1=∠2=∠BAC.求证:△ABE≌△CAF;
(3)如图3,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,求△ACF与△BDE的面积之和.
-
科目: 来源: 题型:
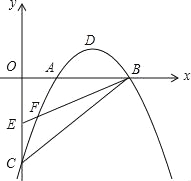
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A(1,0)、B(3,0)两点,与y轴交于点C,其顶点为点D,点E的坐标为(0,﹣1),该抛物线与BE交于另一点F,连接BC.
(1)求该抛物线的解析式,并用配方法把解析式化为y=a(x﹣h)2+k的形式;
(2)若点H(1,y)在BC上,连接FH,求△FHB的面积;
(3)一动点M从点D出发,以每秒1个单位的速度平沿行与y轴方向向上运动,连接OM,BM,设运动时间为t秒(t>0),在点M的运动过程中,当t为何值时,∠OMB=90°?
(4)在x轴上方的抛物线上,是否存在点P,使得∠PBF被BA平分?若存在,请直接写出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
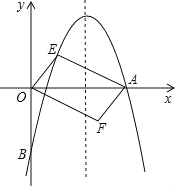
查看答案和解析>>【题目】如图,对称轴为直线x=的抛物线经过点A(6,0)和B(0,﹣4).
(1)求抛物线解析式及顶点坐标;
(2)设点E(x,y)是抛物线上一动点,且位于第一象限,四边形OEAF是以OA为对角线的平行四边形,求平行四边形OEAF的面积S与x之间的函数关系式;
(3)当(2)中的平行四边形OEAF的面积为24时,请判断平行四边形OEAF是否为菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】巴黎与北京的时间差为﹣7时(正数表示同一时刻比北京时间早的时数),如果北京时间是7月2日14:00,那么巴黎时间是( )
A. 7月2日21时 B. 7月2日7时 C. 7月1日7时 D. 7月2日5时
相关试题

