【题目】已知数轴上三点A,O,B表示的数分别为﹣3,0,1,点P为数轴上任意一点,其表示的数为x.
(1)如果点P到点A,点B的距离相等,那么x=;
(2)当x=时,点P到点A,点B的距离之和是6;
(3)若点P到点A,点B的距离之和最小,则x的取值范围是;
(4)在数轴上,点M,N表示的数分别为x1 , x2 , 我们把x1 , x2之差的绝对值叫做点M,N之间的距离,即MN=|x1﹣x2|.若点P以每秒3个单位长度的速度从点O沿着数轴的负方向运动时,点E以每秒1个单位长度的速度从点A沿着数轴的负方向运动、点F以每秒4个单位长度的速度从点B沿着数轴的负方向运动,且三个点同时出发,那么运动秒时,点P到点E,点F的距离相等.
参考答案:
【答案】
(1)-1
(2)﹣4或2
(3)﹣3≤x≤1
(4)![]() 或2
或2
【解析】解:(1)由题意得,|x﹣(﹣3)|=|x﹣1|,
解得x=﹣1;(2)∵AB=|1﹣(﹣3)|=4,点P到点A,点B的距离之和是6,
∴点P在点A的左边时,﹣3﹣x+1﹣x=6,
解得x=﹣4,
点P在点B的右边时,x﹣1+x﹣(﹣3)=6,
解得x=2,
综上所述,x=﹣4或2;(3)由两点之间线段最短可知,点P在AB之间时点P到点A,点B的距离之和最小,
所以x的取值范围是﹣3≤x≤1;(4)设运动时间为t,点P表示的数为﹣3t,点E表示的数为﹣3﹣t,点F表示的数为1﹣4t,
∵点P到点E,点F的距离相等,
∴|﹣3t﹣(﹣3﹣t)|=|﹣3t﹣(1﹣4t)|,
∴﹣2t+3=t﹣1或﹣2t+3=1﹣t,
解得t= ![]() 或t=2.故答案为:(1)﹣1;(2)﹣4或2;(3)﹣3≤x≤1;(4)
或t=2.故答案为:(1)﹣1;(2)﹣4或2;(3)﹣3≤x≤1;(4) ![]() 或2.
或2.
(1)根据数轴上两点间的距离的表示列出方程求解即可;(2)根据AB的距离为4,小于6,分点P在点A的左边和点B的右边两种情况分别列出方程,然后求解即可;(3)根据两点之间线段最短可知点P在点AB之间时点P到点A,点B的距离之和最小最短,然后写出x的取值范围即可;(4)设运动时间为t,分别表示出点P、E、F所表示的数,然后根据两点间的距离的表示列出绝对值方程,然后求解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠A=30°,∠B=50°,则∠C为( )
A. 30° B. 50° C. 80° D. 100°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P(﹣b,2)与点Q(3,2a)关于原点对称,则a= ,b= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种电脑的价格一月份下降了10%,二月份上升了10%,则二月份的价格与原价相比( )
A.不增也不减
B.增加1%
C.减少9%
D.减少1% -
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形内角和是外角和的是4倍,则这个多边形的边数是_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
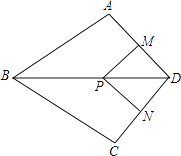
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形. -
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形的两条邻边的比为2:1,周长为60cm,则这个四边形较短的边长为________.
相关试题

