Question

【题目】如图，已知AB为⊙O的直径，AC为⊙O的切线，OC交⊙O于点D，BD的延长线交AC于点E．

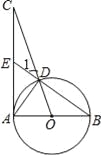
（1）求证：∠1=∠CAD；

（2）若AE=EC=2，求⊙O的半径．

Answer 1

【答案】（1）证明过程见解析；（2）

【解析】试题分析：（1）由AB为⊙O的直径，AC为⊙O的切线，易证得∠CAD=∠BDO，继而证得结论；

（2）由（1）易证得△CAD∽△CDE，然后由相似三角形的对应边成比例，求得CD的长，再利用勾股定理，求得答案．

试题解析：（1）∵AB为⊙O的直径，

∴∠ADB=90°，

∴∠ADO+∠BDO=90°，

∵AC为⊙O的切线，

∴OA⊥AC，

∴∠OAD+∠CAD=90°，

∵OA=OD，

∴∠OAD=∠ODA，

∵∠1=∠BDO，

∴∠1=∠CAD；

（2）∵∠1=∠CAD，∠C=∠C，

∴△CAD∽△CDE，

∴CD：CA=CE：CD，

∴CD2=CACE，

∵AE=EC=2，

∴AC=AE+EC=4，

∴CD=2，

设⊙O的半径为x，则OA=OD=x，

则Rt△AOC中，OA2+AC2=OC2，

∴x2+42=（2+x）2，

解得：x=．

∴⊙O的半径为．