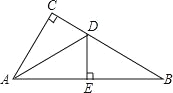
【题目】如图,△ABC 中,∠C=90°,AD 是△ABC 的角平分线,DE⊥AB于 E,AC=BE.
(1)求证:AD=BD;
(2)求∠B的度数.
参考答案:
【答案】(1)证明见解析;(2)∠B=30°.
【解析】
(1)根据角平分线的性质得到 CD=DE,根据全等三角形的判定和性质即可得到结论;
(2)根据角平分线的定义可得∠CAD=∠BAD,根据等边对等角可得∠B=∠BAD,再根据三角形的内角和定理列出方程求解即可.
(1)∵DE⊥AB于E,∠C=90°,AD是△ABC的角平分线,
∴CD=DE,
在Rt△ACD与Rt△AED中,
![]() ,
,
∴Rt△ACD≌Rt△AED,
∴AC=AE,
∵AC=BE,
∴AE=BE,
∴AD=BD;
(2) ∵点D是△ABC的角平分线,
∴∠CAD=∠BAD,
∵AD=BD,
∴∠B=∠BAD,
∴∠CAD=∠BAD=∠B,
∵∠C=90°,
∴∠CAD+∠BAD+∠B=90°,
∴∠B=30°.
-
科目: 来源: 题型:
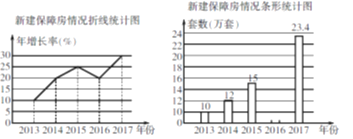
查看答案和解析>>【题目】保障房建设是民心工程,某市从2013年加快保障房建设工程. 现统计该市从2013年到2017年这5年新建保障房情况,绘制成如图所示的折线统计图和不完整的条形统计图.
(1)小颖看了统计图后说:“该市2016年新建保障房的套数比2015年少了.” 你认为小颖的说法正确吗?请说明理由;
(2)求2016年新建保障房的套数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在边长为1的小正方形组成的正方形网格中建立如图所示的平面直角坐标系,已知格点三角形ABC(三角形的三个顶点都在小正方形的顶点上).
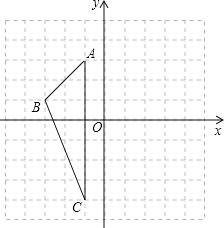
(1)写出△ABC的面积;
(2)画出△ABC关于y轴对称的△A1B1C1;
(3)写出点A及其对称点A1的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某数学老师将本班学生的身高数据(精确到1cm)交给甲、乙两同学,要求他们各自独立地绘制一幅频数直方图,甲绘制的图如图1所示,乙绘制的图如图2所示,经检测确定,甲绘制的频数直方图是正确的,乙在整理数据及绘图过程中均有个别错误.
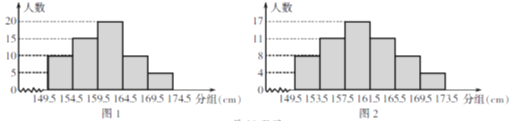
(1)问:该班学生有多少人?
(2)某同学身高为165cm,他说:“我们班上比我高的人不超过
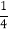 .”他的说法正确吗?
.”他的说法正确吗?(3)请指出乙在整理数据或绘图过程中存在的一个错误.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心,AB为半径的扇形(忽略铁丝的粗细).则所得扇形AFB(阴影部分)的面积为( )
A.6π
B.18
C.18π
D.20 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:点B、F、C、E在一条直线上,FB=CE,AC=DF.能否由上面的已知条件证明AB∥ED?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件,添加到已知条件中,使AB∥ED成立,并给出证明.

供选择的三个条件(请从其中选择一个):
①AB=ED;
②BC=EF;
③∠ACB=∠DFE.
-
科目: 来源: 题型:
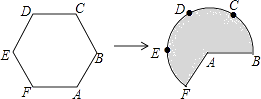
查看答案和解析>>【题目】一个寻宝游戏的寻宝通道如图1所示,通道由在同一平面内的AB,BC,CA,OA,OB,OC组成.为记录寻宝者的行进路线,在BC的中点M处放置了一台定位仪器.设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图象大致如图2所示,则寻宝者的行进路线可能为( )
A.A→O→B
B.B→A→C
C.B→O→C
D.C→B→O
相关试题

