【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 延长线上一点,点
延长线上一点,点![]() 在
在![]() 上.且
上.且![]() .
.

(1)求证:![]() ;
;
(2)若![]() ,则
,则![]() 度数为______.
度数为______.
参考答案:
【答案】(1)见解析;(2)70°
【解析】
(1)由“HL”可证Rt△ABE≌Rt△CBF,可以得到∠BCF=∠BAE,由直角三角形的性质可得结论;
(2)由三角形外角的性质可以得到∠AEB的度数,进而可得到![]() 度数.
度数.
(1)证明:延长AE交CF于H.

∵∠ABC=90°,
∴∠ABE=∠CBF=90°,
在Rt△ABE和Rt△CBF中,
![]() ,
,
∴Rt△ABE≌Rt△CBF(HL);
∴∠BCF=∠BAE,
∵∠BCF+∠F=90°,
∴∠BAE+∠F=90°,
∴∠AHF=90°,
∴AF⊥CF;
(2)![]() ,
,![]() ,
,
∴∠ACB=45°,
∵![]() ,
,
∴∠AEB=70°,
∵Rt△ABE≌Rt△CBF,
∴![]() =∠AEB=70°.
=∠AEB=70°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】夏季的一天,身高为1.6m的小玲想测量一下屋前大树的高度,她沿着树影BA由B到A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,于是得出树的高度为( )

A.8m B.6.4m C.4.8m D.10m
【答案】A.
【解析】
试题分析:因为人和树均垂直于地面,所以和光线构成的两个直角三角形相似,
设树高x米,则
 ,即
,即 ,解得,x=8. 故选A.
,解得,x=8. 故选A.考点:相似三角形的应用.
【题型】单选题
【结束】
11【题目】已知圆锥的底面半径为1cm,母线长为3cm,则其全面积为________cm2 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(3,﹣6)是二次函数y=ax2上的一点,则这二次函数的解析式是 .
【答案】y=﹣
 x2
x2【解析】
试题分析:将点A(3,﹣6)代入y=ax2,利用待定系数法法求该二次函数的解析式即可得﹣6=9a,
解得a=﹣
 ;因此该二次函数的解析式为:y=﹣
;因此该二次函数的解析式为:y=﹣ x2.
x2.考点:待定系数法求二次函数解析式
【题型】填空题
【结束】
15【题目】在一个不透明的口袋中装有8个红球和若干个白球,它们除颜色外其它完全相同,通过多次摸球试验后发现,摸到红球的频率稳定在40%附近,则口袋中白球可能有________个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 的三个顶点坐标为
的三个顶点坐标为 ,
, ,
, .
.
(1)将
 绕坐标原点
绕坐标原点 逆时针旋转
逆时针旋转 ,画出对应图形
,画出对应图形 ,
,(2)并写出点
 的对应点
的对应点 的坐标______;点
的坐标______;点 关于原点对称的对应点
关于原点对称的对应点 坐标_______;
坐标_______;(3)请直接写出:以
 、
、 、
、 为顶点的平行四边形的第四个顶点
为顶点的平行四边形的第四个顶点 的坐标______.
的坐标______. -
科目: 来源: 题型:
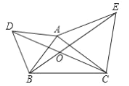
查看答案和解析>>【题目】如图,
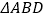 与
与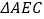 都是等边三角形,
都是等边三角形,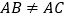 ,下列结论中,正确的个数是( )①
,下列结论中,正确的个数是( )①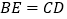 ;②
;②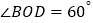 ;③
;③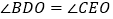 ;④若
;④若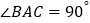 ,且
,且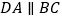 ,则
,则 .
.
A.1B.2C.3D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:已知点A、B是反比例函数y=﹣
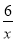 上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.
上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:已知点A、B是反比例函数y=﹣
 上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.
上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.
【答案】

【解析】过点A作AD⊥y轴于点D,过点B作BE⊥y轴于点E,过点A作AF⊥BE轴于点F,如图所示.

∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
又∵AD⊥y轴,BE⊥y轴,
∴∠ACD+∠CAD=90°,∠BCE+∠CBE=90°,
∴∠ACD=∠CBE,∠BCE=∠CAD.
在△ACD和△CBE中,由
 ,
,∴△ACD≌△CBE(ASA).
设点B的坐标为(m,﹣
 )(m<0),则E(0,﹣
)(m<0),则E(0,﹣ ),点D(0,3﹣m),点A(﹣
),点D(0,3﹣m),点A(﹣ ﹣3,3﹣m),
﹣3,3﹣m),∵点A(﹣
 ﹣3,3﹣m)在反比例函数y=﹣
﹣3,3﹣m)在反比例函数y=﹣ 上,
上, ,解得:m=﹣3,m=2(舍去).
,解得:m=﹣3,m=2(舍去).∴点A的坐标为(﹣1,6),点B的坐标为(﹣3,2),点F的坐标为(﹣1,2),
∴BF=2,AF=4,

故答案为:2
 .
.【点睛】
过点A作AD⊥y轴于点D,过点B作BE⊥y轴于点E,过点A作AF⊥BE轴于点F,根据角的计算得出“∠ACD=∠CBE,∠BCE=∠CAD”,由此证出△ACD≌△CBE;再设点B的坐标为(m,﹣
 ),由三角形全等找出点A的坐标,将点A的坐标代入到反比例函数解析式中求出m的值,将m的值代入A,B点坐标即可得出点A,B的坐标,并结合点A,B的坐标求出点F的坐标,利用勾股定理即可得出结论.
),由三角形全等找出点A的坐标,将点A的坐标代入到反比例函数解析式中求出m的值,将m的值代入A,B点坐标即可得出点A,B的坐标,并结合点A,B的坐标求出点F的坐标,利用勾股定理即可得出结论.【题型】填空题
【结束】
18【题目】二次函数y=x2+(2m+1)x+(m2﹣1)有最小值﹣2,则m=________.
相关试题

