【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,交y轴于C点,其中B点坐标为(3,0),C点坐标为(0,3),且图象对称轴为直线x=1.
(1)求此二次函数的关系式;
(2)P为二次函数y=ax2+bx+c图象上一点,且S△ABP=S△ABC,求P点的坐标.

参考答案:
【答案】(1)二次函数的表达式为y=﹣x2+2x+3;(2)P点的坐标为(2,3)或(1﹣![]() ,﹣3)或(1+
,﹣3)或(1+![]() ,﹣3).
,﹣3).
【解析】试题分析:(1)将B、C的坐标和对称轴方程代入抛物线的解析式中,即可求得待定系数的值,可得此二次函数的关系式;
(2)根据等底等高的三角形的面积相等,可得P的纵坐标与C的纵坐标相等或互为相反数,根据自变量与函数值的对应关系,可得答案.
试题解析:解:(1)根据题意,得: 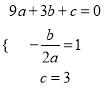 ,解得:
,解得:  .
.
故二次函数的表达式为y=﹣x2+2x+3.
(2)由S△ABP=S△ABC,得yP=3或﹣3,当y=3时,x=2;当y=﹣3时,﹣x2+2x+3=﹣3,
解得x1=![]() ,x2=
,x2=![]() .
.
故P点的坐标为(2,3)或(![]() ,﹣3)或(
,﹣3)或(![]() ,﹣3).
,﹣3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,双曲线y1=
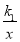 与直线y2=
与直线y2=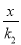 的图象交于A、B两点.已知点A的坐标为(4,1),点P(a,b)是双曲线y1=
的图象交于A、B两点.已知点A的坐标为(4,1),点P(a,b)是双曲线y1=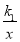 上的任意一点,且0<a<4.
上的任意一点,且0<a<4.(1)分别求出y1、y2的函数表达式;
(2)连接PA、PB,得到△PAB,若4a=b,求三角形ABP的面积;
(3)当点P在双曲线y1=
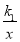 上运动时,设PB交x轴于点E,延长PA交x轴于点F,判断PE与PF的大小关系,并说明理由.
上运动时,设PB交x轴于点E,延长PA交x轴于点F,判断PE与PF的大小关系,并说明理由.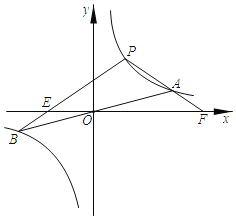
-
科目: 来源: 题型:
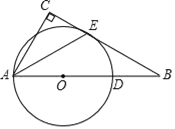
查看答案和解析>>【题目】如图,Rt△ABC,∠C=90°,点D为AB上的一点,以AD为直径的⊙O与BC相切于点E,连接AE.
(1)求证:AE平分∠BAC;
(2)若AC=8,OB=18,求BD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市某工厂现有甲种原料360千克,乙种原料290千克,计划用这两种原料全部生产A,B两种产品共50件,生产A,B两种产品与所需原料情况如下表所示:
原料
型号
甲种原料(千克)
乙种原料(千克)
A产品(每件)
9
3
B产品(每件)
4
10
(1)该工厂生产A,B两种产品有哪几种方案?
(2)如果该工厂生产一件A产品可获利80元,生产一件B产品可获利120元,那么该工厂应该怎样安排生产可获得最大利润?
-
科目: 来源: 题型:
查看答案和解析>>【题目】“莲城读书月”活动结束后,对八年级(三)班45人所阅读书籍数量情况的统计结果如下表所示:
阅读数量
1本
2本
3本
3本以上
人数(人)
10
18
13
4
根据统计结果,阅读2本书籍的人数最多,这个数据2是( )
A.平均数 B.中位数 C.众数 D.方差
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,转盘中8个扇形的面积都相等,任意转动转盘1次,当转盘停止转动时,估计下列事件发生的可能性的大小,并将这些事件的序号按发生的可能性从小到大的顺序排成一列是__________.(填序号)

(1)指针落在标有3的区域内;(2)指针落在标有9的区域内;
(3)指针落在标有数字的区域内;(4)指针落在标有奇数的区域内.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店购进一种商品,每件商品进价30元.试销中发现这种商品每天的销售量y(件)与每件销售价x(元)的关系数据如下:
x
30
32
34
36
y
40
36
32
28
(1)已知y与x满足一次函数关系,根据上表,求出y与x之间的关系式.(不写出自变量x的取值范围);
(2)如果商店销售这种商品,每天要获得150元,那么每件商品的销售价应定为多少元?
(3)设该商店每天销售这种商品所获利润为w(元),求出w与x之间的关系式,并求出每件商品销售价定为多少元时利润最大?
相关试题

