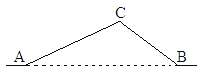
【题目】如图,从A地到B地的公路需要经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°。因城市规划的需要,将在A,B两地之间修建一条笔直的公路。
(1)求改直后的公路AB的长;
(2)问:公路改造后比原来缩短了多少千米?
(sin25°≈0.42,cos25°≈0.91,sin37°≈0.60,tan37°≈0.75)
参考答案:
【答案】(1)AB= 14.7(千米)(2)改直后的路程缩短了2.3千米
【解析】
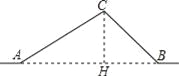
试题(1)、作CH⊥AB于H.在Rt△ACH中,根据三角函数求得CH,AH,在Rt△BCH中,根据三角函数求得BH,再根据AB=AH+BH即可求解;(2)、在Rt△BCH中,根据三角函数求得BC,再根据AC+BC﹣AB列式计算即可求解.
试题解析:(1)、作CH⊥AB于H. 在Rt△ACH中,CH=ACsin∠CAB=ACsin25°≈10×0.42=4.2(千米),
AH=ACcos∠CAB=ACcos25°≈10×0.91=9.1(千米),
在Rt△BCH中,BH=CH÷tan∠CBA=4.2÷tan37°≈4.2÷0.75=5.6(千米),
∴AB=AH+BH=9.1+5.6=14.7(千米). 故改直的公路AB的长14.7千米;
(2)、在Rt△BCH中,BC=CH÷sin∠CBA=4.2÷sin37°≈4.2÷0.6=7(千米),
则AC+BC﹣AB=10+7﹣14.7=2.3(千米). 答:公路改直后比原来缩短了2.3千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,台风中心位于点P,并沿东北方向PQ移动,已知台风移动的速度为30 km/h,受影响区域的半径为200 km,B市位于点P的北偏东75°方向上,距离点P 320 km处.本次台风是否会影响B市?若影响,求出这次台风影响B市的时间;若不影响,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形中有3个角、3条边共6个元素,由其中的已知元素,求出所有未知元素的过程,叫做解三角形.
已知△ABC中,AB=
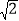 ,∠B=45°,BC=1+
,∠B=45°,BC=1+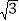 ,解△ABC.
,解△ABC.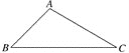
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=12,BC=16,将矩形ABCD沿EF折叠,使点B与点D重合,则折痕EF的长为( )
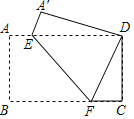
A.14B.
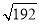 C.
C.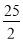 D.15
D.15 -
科目: 来源: 题型:
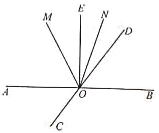
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,∠BOE=90°,OM平分∠AOD,ON平分∠DOE.
(1)若∠MOE=27°,求∠AOC的度数;
(2)当∠BOD=x°(0<x<90)时,求∠MON的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,D为斜边AB的中点,动点P从B出发,沿B→C→A运动,如图(1)所示,设S△DPB=y,点P运动的路程为x,若y与x之间的函数关系图象如图(2)所示,则图(2)中Q点的坐标是( )
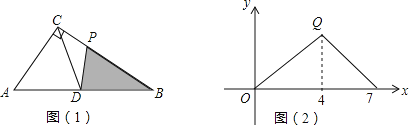
A. (4,2) B. (4,3) C. (4,4) D. (4,6)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,OC边在x轴上点A、D、C共线,反比例函数y=
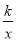 在第一象限的图象经过点B,则△OAC和△BAD的面积之差为_____(用含k的代数式表示).
在第一象限的图象经过点B,则△OAC和△BAD的面积之差为_____(用含k的代数式表示).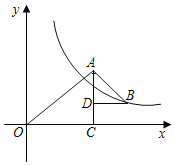
相关试题

