【题目】如图所示,在△ABC中,∠C=90°,AC=6cm,BC=8cm,
点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点
B以2cm/s的速度移动.
(1)如果P、Q同时出发,几秒钟后,可使△PCQ的面积为8平方厘米?
(2)点P、Q在移动过程中,是否存在某一时刻,使得△PCQ的面积等于
△ABC的面积的一半.若存在,求出运动的时间;若不存在,说明理由.

参考答案:
【答案】(1)2s或4s;(2)不存在.理由参见解析.
【解析】
试题分析:(1)设xs后,可使△PCQ的面积为8cm2,则PC=(6-x)cm,CQ=2xcm.根据三角形面积公式建立一元二次方程求解;(2)列△PCQ的面积等于△ABC面积的一半.建立一元二次方程,根据根的判别式,确定此方程是否有解,从而判断是否存在使△PCQ的面积等于ABC面积一半的时刻.
试题解析:(1)设xs后,可使△PCQ的面积为8cm2,所以 AP=xcm,PC=(6-x)cm,CQ=2xcm.则根据题意,得![]() ·(6-x)·2x=8.整理,得x2-6x+8=0,解这个方程,得x1=2,x2=4. 所以P、Q同时出发,2s或4s后可使△PCQ的面积为8cm2;(2)设点P出发x秒后,△PCQ的面积等于△ABC面积的一半.则根据题意,得
·(6-x)·2x=8.整理,得x2-6x+8=0,解这个方程,得x1=2,x2=4. 所以P、Q同时出发,2s或4s后可使△PCQ的面积为8cm2;(2)设点P出发x秒后,△PCQ的面积等于△ABC面积的一半.则根据题意,得![]() (6-x)·2x=
(6-x)·2x=![]() ×
×![]() ×6×8.整理,得x2-6x+12=0. 由于根的判别式小于0, 所以此方程没有实数根,所以不存在使△PCQ的面积等于ABC面积一半的时刻.
×6×8.整理,得x2-6x+12=0. 由于根的判别式小于0, 所以此方程没有实数根,所以不存在使△PCQ的面积等于ABC面积一半的时刻.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知AB=AC,D为∠BAC的平分线上面-点.连接BD,CD;全等三角形的对数是______
如图2.已知AB=AC,D,E为∠BAC的平分线上面两点.连接BD,CD,BE,CE;全等三角形的对数是___________
如图3.已知AB=AC,D,E,F为∠BAC的平分线上面三点,连接BD,CD,BE,CE,BF,CF;全等三角形的对数是_______________
…
依此规律,第n个图形中有全等三角形的对数是 __________

-
科目: 来源: 题型:
查看答案和解析>>【题目】﹣12的值是( )
A.1
B.-1
C.2
D.-2 -
科目: 来源: 题型:
查看答案和解析>>【题目】地球的半径为6.4×103km,这个近似数精确到( )
A. 个位 B. 十分位 C. 十位 D. 百位
-
科目: 来源: 题型:
查看答案和解析>>【题目】气温上升5℃记做+5℃,那么﹣5℃表示__.
-
科目: 来源: 题型:
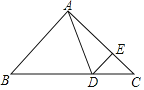
查看答案和解析>>【题目】如图,在△ABC中,∠B=∠C=45°,点D在BC边上,点E在AC边上,且∠ADE=∠AED,连结DE.
(1)当∠BAD=60°,求∠CDE的度数;
(2)当点D在BC(点B、C除外)边上运动时,试写出∠BAD与∠CDE的数量关系,并说明理由.
-
科目: 来源: 题型:
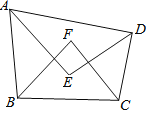
查看答案和解析>>【题目】如图,四边形ABCD的内角∠BAD、∠CDA的角平分线交于点E,∠ABC、∠BCD的角平分线交于点F.
(1)若∠F=70°,则∠ABC+∠BCD= ______ °;∠E= ______ °;
(2)探索∠E与∠F有怎样的数量关系,并说明理由;
(3)给四边形ABCD添加一个条件,使得∠E=∠F,所添加的条件为______.
相关试题

