【题目】如图,已知BA⊥AC,CD⊥DB,AC与BD交于O,BD=CA.
求证:⑴ BA=CD; ⑵ △OBC是等腰三角形.

参考答案:
【答案】(1)详见解析;(2)详见解析.
【解析】试题分析:
(1)由已知易证△ABC和△DCB都是直角三角形,利用BD=CA,BC=CB可由“HL”证得两三角形全等,从而可得BA=CD;
(2)由(1)中所证△ABC≌△DCB可得∠ACB=∠DBC,从而可得OB=OC.
试题解析:
(1) ∵ BA⊥AC,CD⊥DB
∴∠A=∠D=90°
在Rt△ABC和Rt△DCB中: ![]() ,
,
∴ △ABC≌△DCB (HL).
∴ BA=CD.
⑵ ∵ △ABC≌△DCB,
∴ ∠ACB=∠DBC.
∴ BO=CO.
∴ △OBC是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某星期天小李步行取图书馆看书,途中遇到一个红灯,停下来耽误了几分钟,为了赶时间,他以更快速度步行到图书馆,下面几幅图是步行路程s(米)与行进时间t(分)的关系的示意图,你认为正确的是( )
A.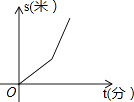
B.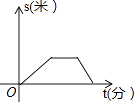
C.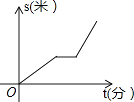
D.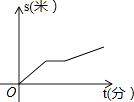
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:
①任何正数的两个平方根的和等于0;
②任何实数都有一个立方根;
③无限小数都是无理数;
④实数和数轴上的点一一对应.
其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们把使得函数值为零的自变量的值称为函数的零点. 例如,对于函数y=-x+1,令y=0,可得x=1,我们就说x=1是函数y=-x+1的零点.己知函数y=x2-2(m+1)x-2(m+2)
(m为常数) .(1)当m=-1时,求该函数的零点;
(2)证明:无论m取何值,该函数总有两个零点;
(3)设函数的两个零点分别为
 和
和 ,且
,且 ,求此时的函数解析式,并判断点(n+2,n2-10)是否在此函数的图象上.
,求此时的函数解析式,并判断点(n+2,n2-10)是否在此函数的图象上. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个多项式是五次多项式,那么( )
A. 这个多项式至少有一项的次数是5 B. 这个多项式只能有一项的次数是5
C. 这个多项式一定是五次六项式 D. 这个多项式最多有六项
-
科目: 来源: 题型:
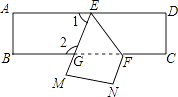
查看答案和解析>>【题目】把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D,C分别在M,N的位置上,若∠EFG=56°,则∠1= , ∠2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x1=3是关于x的一元二次方程x2-4x+c=0的一个根,则方程的另一个根x2是。
相关试题

