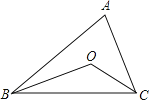
【题目】点O是△ABC内一点,且点O到三边的距离相等,∠A=60°,则∠BOC的度数为( )
A.60°B.90°C.120°D.150°
参考答案:
【答案】C
【解析】
根据三角形内角和定理求出∠ABC+∠ACB=120°,再根据角平分线上的点到角的两边的距离相等判断出点O是△ABC角平分线的交点,再根据角平分线的定义求出∠OBC+∠OCB的度数,然后在△OBC中,利用三角形内角和定理列式进行计算即可得解.
∵点O是△ABC内一点,且O到三边的距离相等,
∴O是△ABC的内切圆的圆心,即为△ABC内角平分线的交点,
∴∠OCB=![]() ∠ACB,∠OBC=
∠ACB,∠OBC=![]() ∠ABC,
∠ABC,
∵∠A=60°,
∴∠ABC+∠ACB=180°-∠A=120°,
∴∠OBC+∠OCB =![]() (∠ABC+∠ACB)=60°,
(∠ABC+∠ACB)=60°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-60°=120°,故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小强家有一块三角形菜地,量得两边长分别为
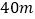 ,
,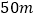 ,第三边上的高为
,第三边上的高为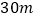 .请你帮小强计算这块菜地的面积.(结果保留根号)
.请你帮小强计算这块菜地的面积.(结果保留根号) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
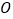 为等边三角形
为等边三角形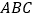 内一点,连接
内一点,连接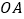 ,
,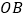 ,
,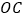 ,以
,以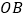 为一边作
为一边作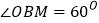 ,且
,且 ,连接
,连接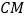 、
、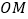 .
. (1)判断
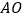 与
与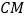 的大小关系并证明;
的大小关系并证明; (2)若
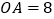 ,
,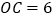 ,
,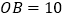 ,判断
,判断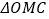 的形状并证明.
的形状并证明.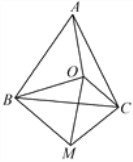
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,点 E、F分别为边 AD、CD上的动点(都与菱形的顶点不重合),联结 EF、BE、BF .
(1)若∠A=60°,且 AE+CF=AB,判断△BEF 的形状,并说明理由;
(2)在(1)的条件下,设菱形的边长为a,求△BEF面积的最小值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是 ( )

A.
 B. 2
B. 2 C. 3 D. 2
C. 3 D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB⊥BC,BE⊥AC,∠1=∠2,AD=AB,则下列结论不正确的是
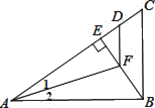
A. BF=DF B. ∠1=∠EFD C. BF>EF D. FD∥BC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②BF=BA;③PH=PD;④连接CP,CP平分∠ACB,其中正确的是( )

A. ①②③ B. ①②④ C. ①③④ D. ①②③④
相关试题

