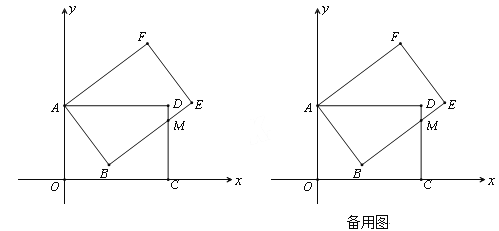
【题目】矩形AOCD绕顶点A(0，5)逆时针方向旋转，当旋转到如图所示的位置时，边BE交边CD于M，且ME=2，CM=4.

（1）求AD的长；

（2）求经过A、B、D三点的抛物线的解析式；

（3）在直线AM下方，（2）中的抛物线上是否存在点P，使S△PAM =？若存在，求出P点坐标；若不存在，请说明理由．

参考答案：

【答案】（1）AD=7；（2）；（3）P点坐标为（3，1）、（，）

【解析】试题分析: （1）作BP⊥AD于P，BQ⊥MC于Q，根据旋转的性质得AB=AO=5，BE=OC=AD，∠ABE=90°，利用等角的余角相等得∠ABP=∠MBQ，可证明Rt△ABP∽Rt△MBQ得到，设BQ=PD=x，AP=y，则AD=x+y，所以BM=x+y-2，利用比例性质得到PBMQ=xy，而PB-MQ=DQ-MQ=DM=1，利用完全平方公式和勾股定理得到52-y2-2xy+（x+y-2）2-x2=1，解得x+y=7，则BM=5，BE=BM+ME=7，所以AD=7；

（2）由AB=BM可判断Rt△ABP≌Rt△MBQ，则BQ=PD=7-AP，MQ=AP，利用勾股定理得到（7-MQ）2+MQ2=52，解得MQ=4（舍去）或MQ=3，则BQ=4，根据三角形面积公式和梯形面积公式，利用S阴影部分=S梯形ABQD-S△BQM进行计算即可；然后利用待定系数法求直线AM的解析式.先确定B（3，1），然后利用待定系数法求抛物线的解析式；

（3）当点P在线段AM的下方的抛物线上时，作PK∥y轴交AM于K，如图2设P（x，x2-x+5），则K（x，-x+5），则KP=-x2+x，根据三角形面积公式得到（-x2+x）7=，解得x1=3，x2=，于是得到此时P点坐标为（3，1）、（，）；再求出过点（3，1）与（，）的直线l的解析式为y=-x+，则可得到直线l与y轴的交点A′的坐标为（0，），所以AA′=，然后把直线AM向上平移个单位得到l′，直线l′与抛物线的交点即为P点，由于A″（0，），则直线l′的解析式为y=-x+，再通过解方程组得P点坐标．

试题解析:

解：⑴ 如图1，连接AM，

在矩形AOCD中，∠AOC=∠ADC=90°，AD=OC，CD=AO=5，

∵CM=4，

∴DM=1，

由旋转，得∠B=∠AOC =90°，BE=OC，AB=AO=5，

设BE=OC= AD=x，

在Rt△ADM中，AM2=x2+1，

在Rt△ABM中，AM2=(x-2) 2+25,

∴x2+1=(x-2) 2+25，解得x=7，

∴AD=7.

⑵ 如图2，过点B作x轴的平行线，交AO于G，交DC于H，

则 ∠AGB=∠BHM =90°，

∴ ∠ABG＋∠BAG =90°，

∵ ∠ABE=90°，

∴ ∠ABG＋∠MBH =90°，

∴ ∠BAG =∠MBH ，

∵ AB=BM=5，

∴ △AGB≌△BHM（AAS），

∴ BH=AG，MH=BG，

设MH=BG=n，则DH=n＋1，∴BH=AG=n＋1，

∵ GH=OC=AD=7，

∴ n＋（n＋1）=7，

∴ n=3，

∴ AG=4，BG=3，

∵ A（0，5），

∴ 点B的坐标为（3，1），

设经过A、B、D三点的抛物线的解析式为y=ax+bx+5，将B（3，1），

D（7，5）代入，得

解得

∴y=x2-x+5.

图2

⑶ 存在．

设直线AM的解析式为y=kx+5，将M（7，4）代入，得k=，

∴y=-x+5,

∵点P在线段AD的下方的抛物线上，作PK∥y轴交AM于K，

设P（x，），则K（x，），

∴KP=﹣=，

∵S△PAM=，

∴7=，

整理得7x2﹣46x+75=0，

解得x1=3，x2=，

此时P点坐标为（3，1）、（，）.

点睛: 本题考查了几何变换综合题：熟练掌握旋转的性质、矩形的性质和三角形全等于相似的判定与性质；会利用待定系数法求函数解析式；理解坐标与图形性质；会进行代数式的变形．

关闭