【题目】已知:如图,在△ABC中,DE∥BC,AD2=AEAC.求证: 
(1)△BCD∽△CDE;
(2)![]() .
.
参考答案:
【答案】
(1)证明:∵AD2=AEAC,
∴ ![]() ,
,
∵∠A是公共角,
∴△ADC∽△AED,
∴∠ACD=∠ADE,
∵DE∥BC,
∴∠ADE=∠B,∠BCD=∠CDE,
∴∠ECD=∠B,
∴△BCD∽△CDE
(2)证明:∵△BCD∽△CDE,
∴ ![]() ,
,
∴DE= ![]() ,
,
∵DE∥BC,
∴△ADE∽△ABC,
∴ ![]() ,
,
∴ ![]()
【解析】(1)由AD2=AEAC,易证得△ADC∽△AED,即可得∠ACD=∠ADE,又由DE∥BC,易证得∠ECD=∠B,则可证得△BCD∽△CDE;(2)由△BCD∽△CDE,根据相似三角形的对应边成比例,即可得 ![]() ,又由DE∥BC,可得△ADE∽△ABC,即可得
,又由DE∥BC,可得△ADE∽△ABC,即可得 ![]() ,继而得到结论.
,继而得到结论.
【考点精析】关于本题考查的相似三角形的判定与性质,需要了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与反比例函数y=
 的图象交于点A(﹣2,﹣5 ),C (5,n),交y轴于点B,交x轴于点D,那么不等式kx+b﹣
的图象交于点A(﹣2,﹣5 ),C (5,n),交y轴于点B,交x轴于点D,那么不等式kx+b﹣  >0的解集是 .
>0的解集是 . 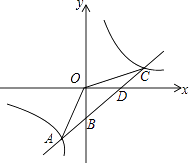
-
科目: 来源: 题型:
查看答案和解析>>【题目】乘法公式的探究及应用:

(1)如图,可以求出阴影部分的面积是_____(写成两数平方差的形式);
(2)如图,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是_____,长是_____,面积是________(写成多项式乘法的形式);
(3)比较左、右两图的阴影部分面积,可以得到乘法公式:_________(用式子表达);
(4)运用你所得到的公式,计算下列式子:(2m+n﹣p)(2m﹣n+p)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,四边形ABCD中,AB∥CD,∠ADC=90°,P从A点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P点的运动时间为t秒,△PAD的面积为S,S关于t的函数图象如图②所示,当P运动到BC中点时,△PAD的面积为 .
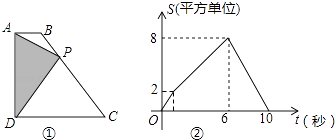
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次函数y=kx-6中,已知y随x的增大而减小.下列关于反比例函数y=

的描述,其中正确的是( )
A. 当x>0时,y>0 B. y随x的增大而增大
C. y随x的增大而减小 D. 图像在第二、四象限
-
科目: 来源: 题型:
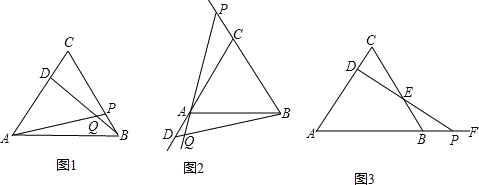
查看答案和解析>>【题目】(9分)探究题:如图:
(1)△ABC为等边三角形,动点D在边CA上,动点P在边BC上,若这两点分别从C、B点同时出发,以相同的速度由C向A和由B向C运动,连接AP,BD交于点Q,两点运动过程中AP=BD成立吗?请证明你的结论;
(2)如果把原题中“动点D在边CA上,动点P边BC上,”改为“动点D,P在射线CA和射线BC上运动”,其他条
件不变,如图(2)所示,两点运动过程中∠BQP的大小保持不变.请你利用图(2)的情形,
求证:∠BQP=60°;
(3)如果把原题中“动点P在边BC上”改为“动点P在AB的延长线上运动,连接PD交BC于E”,其他条件不变,如图(3),则动点D,P在运动过程中,DE始终等于PE吗?写出证明过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某国发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作,如图,某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米,参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,
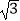 ≈1.7)
≈1.7) 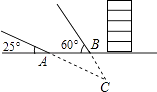
相关试题

