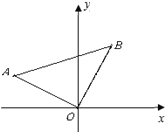
【题目】在平面直角坐标系中,△AOB的位置如图所示,已知∠AOB=90°,AO=BO,点A的坐标为(-3,1).
(1)求点B的坐标;
(2)求过A、O、B三点的抛物线的解析式;
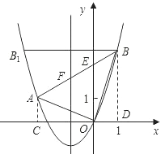
(3)设点B关于抛物线的对称轴![]() 的对称点为B1,求△AB1B的面积.
的对称点为B1,求△AB1B的面积.
参考答案:
【答案】(1)点B的坐标为(1,3);(2)y=![]() x2+
x2+![]() x;(3)
x;(3)![]() =
=![]() .
.
【解析】
(1)过点A作AC⊥x轴,垂足为C,作BD⊥x轴垂足为D,可证明△AOC≌△BOD,则B点的横坐标即为A点的坐标轴,B的纵坐标是A点的横坐标的绝对值,因此可求出B的坐标;(2)已知A,O的坐标,根据(1)求出的B点坐标,用待定系数法求出抛物线的解析式;(3)根据(2)的解析式可得出对称轴的解析式,根据B点坐标得出B1坐标,则BB1就是三角形的底边,B的纵坐标与A的纵坐标的查的绝对值就是△ABB1的高,因此可求出其面积.
(1)过点A作AC⊥x轴,垂足为C,作BD⊥x轴垂足为D,
则∠ACO=∠ODB=90°,
∴∠AOC+∠OAC=90°,
又∠AOB=90°,
∴∠AOC+∠BOD=90°,
∴∠OAC=∠BOD,
又AO=BO,
∴△AOC≌△BOD(AAS)
∴OD=AC=1,DB=OC=3,
∴点B的坐标为(1,3)
(2)因抛物线过原点,
设所求的抛物线解析式为y=ax2+bx,
将A(-3,1),B(1,3)代入
得![]()
解得a=![]() ,b=
,b=![]()
∴所求的抛物线解析式为y=![]() x2+
x2+![]() x;
x;
(3)在y=![]() x2+
x2+![]() x中,对称轴
x中,对称轴![]()
点B1是点B关于抛物线的对称轴![]() 的对称点,
的对称点,
故B1(![]() ,3)
,3)
在△ABB1中,底边B1B=![]() ,高为2,
,高为2,
故S△ABB1=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2020年东京奥运会的比赛门票开始接受公众预订.下表为奥运会官方票务网站公布的几种球类比赛的门票的人民币价格,球迷小李用12000元做为预订下表中比赛项目门票的资金.
比赛项目
票价(元/场)
男篮
1000
足球
800
乒乓球
500
(1)若全部资金用来预订男篮门票和乒乓球门票共15张,问男篮门票和乒乓球门票各订多少张?
(2)若在准备资金允许的范围内和总票数不变的前提下,这个球迷想预定上表中三种球类门票,其中足球门票与乒乓球门票数相同,且足球门票的费用不超过男篮门票的费用,问可以预订这三种球类门票各多少张?
-
科目: 来源: 题型:
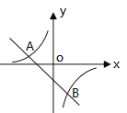
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与反比例函数y=
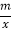 图象交于A(-2,1)、B(1,n)两点.
图象交于A(-2,1)、B(1,n)两点.(1)求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值大于反比例函数的值的x的取值范围。
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家规定“中小学生每天在校体育活动时间不低于1小时”.为此,某市就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图(部分)如图所示,其中分组情况是:
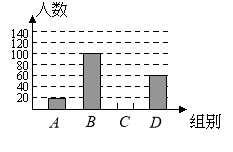
A组:
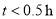 ;B组:
;B组: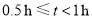
C组:
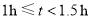 D组:
D组:
请根据上述信息解答下列问题:
(1)C组的人数是;
(2)本次调查数据的中位数落在组内;
(3)若该辖区约有24 000名初中学生,请你估计其中达国家规定体育活动时间的人约有多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图①,②,在矩形ABCD中,AB=4,BC=8,P,Q分别是边BC,CD上的点.
(1)如图①,若AP⊥PQ,BP=2,求CQ的长;
(2)如图②,若
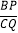 =2,且E,F,G分别为AP,PQ,PC的中点,求四边形EPGF的面积.
=2,且E,F,G分别为AP,PQ,PC的中点,求四边形EPGF的面积.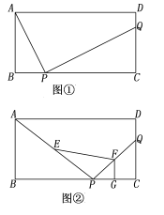
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,②,在平面直角坐标系xoy中,点A的坐标为(4,0),以点A为圆心,4为半径的圆与x轴交于O,B两点,OC为弦,
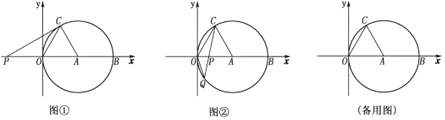 , P是x轴上的一动点,连结CP。
, P是x轴上的一动点,连结CP。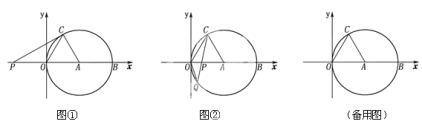
(1)求
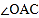 的度数;
的度数;(2)如图①,当CP与⊙A相切时,求PO的长;
(3)如图②,当点P在直径OB上时,CP的延长线与⊙A相交于点Q,问PO为何值时,
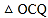 是等腰三角形?
是等腰三角形? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,∠A=20°.将△ABC绕点C按逆时针方向旋转得△A′B′C,且点B在A′B′ 上,CA′ 交AB于点D,则∠BDC的度数为( )
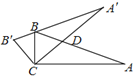
A. 40°B. 50°C. 60°D. 70°
相关试题

