搜索
【题目】四边形ABCD是正方形，E、F分别是DC和CB的延长线上的点，且DE=BF，连接AE、AF、EF．
（1）求证：△ADE≌△ABF；
（2）若BC=8，DE=6，求△AEF的面积．
参考答案：
【答案】（1）证明见解析；（2）50.
【解析】试题分析：（1）利用正方形性质得到边相等角相等，利用SAS证明△ADE≌△ABF.
(2)利用勾股定理计算AE长度，再利用（1）的结论，易得△AEF是等腰直角三角形，求△AEF.的面积
试题解析：
（1）证明：∵四边形ABCD是正方形，
∴AD=AB，∠D=∠ABC=90°，
而F是CB的延长线上的点，
∴∠ABF=90°，
在△ADE和△ABF中，
∴△ADE≌△ABF（SAS）；
（2）解：∵BC=8，
∴AD=8，
在Rt△ADE中，DE=6，AD=8，
∴AE=
=10，
∵△ABF可以由△ADE绕旋转中心 A点，按顺时针方向旋转90度得到，
∴AE=AF，∠EAF=90°，
∴△AEF的面积=
AE2=
×100=50．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图是某公园的一角，∠AOB=90°，弧AB的半径OA长是6米，C是OA的中点，点D在弧AB上，CD∥OB，则图中休闲区（阴影部分）的面积是（ ）
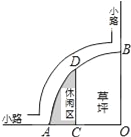
A. （10π﹣
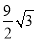）米2 B. （π﹣
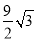）米2 C. （6π﹣
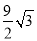）米2 D. （6π﹣
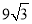）米2 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c图象的一部分，其对称轴为x=﹣1，且过点（﹣3，0）．下列说法：①abc＜0；②2a﹣b=0；③4a+2b+c＜0；④若（﹣5，y1），（
，y2）是抛物线上两点，则y1＞y2．其中说法正确的是（ ）
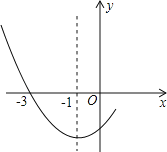
A. ①② B. ②③ C. ①②④ D. ②③④
-
科目： 来源： 题型：
查看答案和解析>>【题目】作图题：（不要求写作法）如图，在 10×10 的方格纸中，有一个格点四边形 ABCD（即四边形的顶点都在格点上）。①在给出的方格纸中，画出四边形 ABCD 向下平移 5 格后的四边形 A
BCD;②在给出的方格纸中，画出四边形 ABCD 关于直线 l 对称的图形 A
BCD.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在如图所示平面直角坐标系中，每个小正方形的边长均为1，△ABC的三个顶点均在格点上．
（1）以O为旋转中心，将△ABC逆时针旋转90°，画出旋转后的△A1B1C1；
（2）画出△A1B1C1关于原点对称的△A2B2C2；
（3）若△ABC内有一点P（a，b），结果上面两次变换后点P在△A2B2C2中的对应点为P′，则点P′的坐标为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）阅读下文，寻找规律：
已知 x≠1 时，（1－x)（1＋x)＝1－x
，(1－x)(1＋x＋x
)＝1－x
，(1－x)(1＋x＋x
＋x)＝1－x
.…观察上式，并猜想：
(1－x)(1＋x＋x
＋ x＋x)＝ ____________. (1－x)(1＋x＋x＋…＋x
)＝ ____________.（2） 通过以上规律，请你进行下面的探素：
①(a－b)(a＋b)＝ ____________.
②(a－b)(a
＋ab＋b)＝ ____________.③(a－b)(a
＋a
＋ab＋b )＝ ____________.（3） 根据你的猜想，计算：
1＋2＋2
＋…＋2
＋2
＋2
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在平面直角坐标系中，已知直线
交
轴于点
，
轴于点
，
的角平分线
交轴于点
，过点作直线
的垂线，交轴于点
．
（1）求直线
的解析式；（2）如图2，若点
为直线上的一个动点，过点作
轴，交直线于点
，当四边形
为菱形时，求
的面积；（3）如图3，点
为轴上的一个动点，连接
、
，将
沿
翻折得到
，当以点、
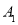、为顶点的三角形是等腰三角形时，求点的坐标．
相关试题
