【题目】如图,过反比例函数y= ![]() (x>0)的图象上任意两点A、B分别作x轴的垂线,垂足分别为C、D,连接OA、OB,设AC与OB的交点为E,△AOE与梯形ECDB的面积分别为S1、S2 , 比较它们的大小,可得( )
(x>0)的图象上任意两点A、B分别作x轴的垂线,垂足分别为C、D,连接OA、OB,设AC与OB的交点为E,△AOE与梯形ECDB的面积分别为S1、S2 , 比较它们的大小,可得( ) 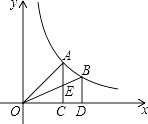
A.S1>S2
B.S1=S2
C.Sl<S2
D.大小关系不能确定
参考答案:
【答案】B
【解析】解:由反比例函数系数k的几何意义可得:S△AOC=S△BOD; 又S△AOC=S△AEO+S△OEC , S△BOD=S△OEC+S梯形CEBD ,
所以S△AOE=S梯形CEBD , 即S1=S2 .
故选B.
【考点精析】利用比例系数k的几何意义对题目进行判断即可得到答案,需要熟知几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
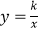 的图象经过点(2,3),下列说法正确的是( )
的图象经过点(2,3),下列说法正确的是( )
A.y随x的增大而增大
B.函数的图象只在第一象限
C.当x<0时,必有y<0
D.点(﹣2,﹣3)不在此函数图象上 -
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)某商场用2500元购进了A、B两种新型节能台灯共50盏,这两种台灯的进价,标价如下表所示:

(1)这两种台灯各购进多少盏?
(2)若A型台灯按标价的九折出售,B型台灯按标价的八折出售,那么这批台灯全部售完后,商场共获利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各数中,比﹣2大的数是( )
A.﹣4B.﹣3C.﹣2D.﹣1
-
科目: 来源: 题型:
查看答案和解析>>【题目】点(3,-4)到x轴的距离为 ( )
A. 3 B. 4 C. 5 D. -4
-
科目: 来源: 题型:
查看答案和解析>>【题目】若xm=4,xn=3,则xm+2n=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一个长为2a、宽为2b的长方形(其中a,b均为正数,且a>b),沿图中虚线用剪刀均匀分成四块相同小长方形,然后按图2方式拼成一个大正方形.
(1)你认为图2中大正方形的边长为 a+b ;小正方形(阴影部分)的边长为 .(用含a、b的代数式表示)
(2)仔细观察图2,请你写出下列三个代数式:(a+b)2,(a-b)2,ab所表示的图形面积之间的相等关系,并选取适合a、b的数值加以验证.
(3)已知a+b=7,ab=6.求代数式(a-b)的值.

相关试题

