【题目】如图,在![]() 中,
中,![]() ,
,![]() .
.
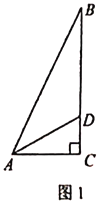
(1)如图1,点![]() 在边
在边![]() 上,
上,![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
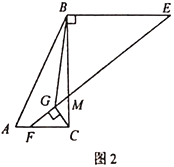
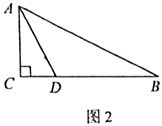
(2)如图2,点![]() 在边
在边![]() 上,过点
上,过点![]() 作
作![]() ,
,![]() ,连结
,连结![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() .求证:
.求证:![]() .
.
参考答案:
【答案】(1)3;(2)见解析.
【解析】
(1)根据勾股定理可得AC,进而可得BC与BD,然后根据三角形的面积公式计算即可;
(2)过点B作BH⊥BG交EF于点H,如图3,则根据余角的性质可得∠CBG=∠EBH,由已知易得BE∥AC,于是∠E=∠EFC,由于![]() ,
,![]() ,则根据余角的性质得∠EFC=∠BCG,于是可得∠E=∠BCG,然后根据ASA可证△BCG≌△BEH,可得BG=BH,CG=EH,从而△BGH是等腰直角三角形,进一步即可证得结论.
,则根据余角的性质得∠EFC=∠BCG,于是可得∠E=∠BCG,然后根据ASA可证△BCG≌△BEH,可得BG=BH,CG=EH,从而△BGH是等腰直角三角形,进一步即可证得结论.
解:(1)在△ACD中,∵![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,
,
∵![]() ,∴BC=4,BD=3,∴
,∴BC=4,BD=3,∴![]() ;
;
(2)过点B作BH⊥BG交EF于点H,如图3,则∠CBG+∠CBH=90°,
∵![]() ,∴∠EBH+∠CBH=90°,∴∠CBG=∠EBH,
,∴∠EBH+∠CBH=90°,∴∠CBG=∠EBH,
∵![]() ,
,![]() ,∴BE∥AC,∴∠E=∠EFC,
,∴BE∥AC,∴∠E=∠EFC,
∵![]() ,
,![]() ,∴∠EFC+∠FCG=90°,∠BCG+∠FCG=90°,
,∴∠EFC+∠FCG=90°,∠BCG+∠FCG=90°,
∴∠EFC=∠BCG,∴∠E=∠BCG,
在△BCG和△BEH中,∵∠CBG=∠EBH,BC=BE,∠BCG=∠E,∴△BCG≌△BEH(ASA),
∴BG=BH,CG=EH,
∴![]() ,
,
∴![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一张矩形纸板按图中虚线裁剪成九块,其中有两块是边长都为
 的大正方形,两块是边长都为
的大正方形,两块是边长都为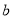 的小正方形,五块是长为
的小正方形,五块是长为 ,宽为
,宽为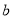 的全等小矩形,且
的全等小矩形,且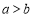 .
.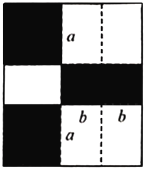
(1)观察图形,将多项式
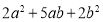 分解因式;
分解因式;(2)若每块小矩形的面积为10,四个正方形的面积和为58.求下列代数式的值:
①
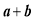 .
.②
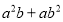 .
. -
科目: 来源: 题型:
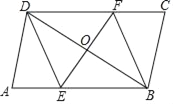
查看答案和解析>>【题目】如图所示,平行四边形形ABCD中,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)请添加一个条件使四边形BEDF为菱形.
-
科目: 来源: 题型:
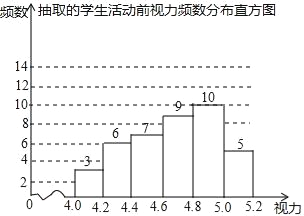
查看答案和解析>>【题目】为了保护视力,学校开展了全校性的视力保健活动,活动前,随机抽取部分学生,检查他们的视力,结果如图所示(数据包括左端点不包括右端点,精确到0.1);活动后,再次检查这部分学生的视力,结果如表所示
分组
频数
4.0≤x<4.2
2
4.2≤x<4.4
3
4.4≤x<4.6
5
4.6≤x<4.8
8
4.8≤x<5.0
17
5.0≤x<5.2
5
(1)求活动所抽取的学生人数;
(2)若视力达到4.8及以上为达标,计算活动前该校学生的视力达标率;
(3)请选择适当的统计量,从两个不同的角度评价视力保健活动的效果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
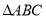 中,
中,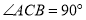 ,点
,点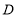 是直线
是直线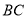 上一点.
上一点.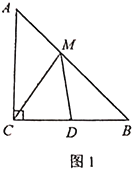
(1)如图1,若
 ,点
,点 是
是 边的中点,点
边的中点,点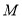 是线段
是线段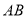 上一动点,求
上一动点,求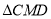 周长的最小值.
周长的最小值.(2)如图2,若
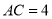 ,
,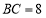 ,是否存在点
,是否存在点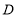 ,使以
,使以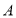 ,
,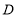 ,
,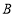 为顶点的三角形是等腰三角形,若存在,请直按写出线段
为顶点的三角形是等腰三角形,若存在,请直按写出线段 的长度:若不存在,请说明理由.
的长度:若不存在,请说明理由. -
科目: 来源: 题型:
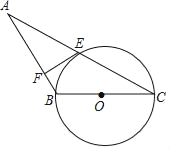
查看答案和解析>>【题目】如图所示,在△ABC中,AB=CB,以BC为直径的⊙O交AC于点E,过点E作⊙O的切线交AB于点F.
(1)求证:EF⊥AB;
(2)若AC=16,⊙O的半径是5,求EF的长.
相关试题

