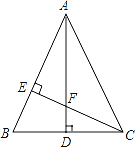
【题目】如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.
求证:(1)△AEF≌△CEB;
(2)AF=2CD.
参考答案:
【答案】(1)证明详见解析;(2)证明详见解析.
【解析】
试题分析:(1)由AD⊥BC,CE⊥AB,易得∠AFE=∠B,利用全等三角形的判定得△AEF≌△CEB;
(2)由全等三角形的性质得AF=BC,由等腰三角形的性质“三线合一”得BC=2CD,等量代换得出结论.
试题解析:(1)∵AD⊥BC,CE⊥AB,
∴∠BCE+∠CFD=90°,∠BCE+∠B=90°,
∴∠CFD=∠B,
∵∠CFD=∠AFE,
∴∠AFE=∠B
在△AEF与△CEB中,
∠AFE=∠B,∠AEF=∠CEB,AE=CE,
∴△AEF≌△CEB(AAS);
(2)∵AB=AC,AD⊥BC,
∴BC=2CD,
∵△AEF≌△CEB,
∴AF=BC,
∴AF=2CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了提高服务质量,某宾馆决定对甲、乙两种套房进行星级提升,已知甲种套房提升费用比乙种套房提升费用少3万元,如果提升相同数量的套房,甲种套房费用为625万元,乙种套房费用为700万元.
(1)甲、乙两种套房每套提升费用各多少万元?
(2)如果需要甲、乙两种套房共80套,市政府筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于甲、乙种套房星级提升,市政府对两种套房的提升有几种方案?哪一种方案的提升费用最少?
(3)在(2)的条件下,根据市场调查,每套乙种套房的提升费用不会改变,每套甲种套房提升费用将会提高a万元(a>0),市政府如何确定方案才能使费用最少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD和CD分别平分△ABC的内角∠EBA和外角∠ECA,BD交AC于F,连接AD.
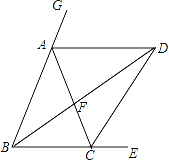
(1)求证:∠BDC=
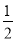 ∠BAC;
∠BAC;(2)若AB=AC,请判断△ABD的形状,并证明你的结论;
(3)在(2)的条件下,若AF=BF,求∠EBA的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AD=acm,AB=bcm(a>b>4),半径为2cm的⊙O在矩形内且与AB、AD均相切,现有动点P从A点出发,在矩形边上沿着A→B→C→D的方向匀速移动,当点P到达D点时停止移动.⊙O在矩形内部沿AD向右匀速平移,移动到与CD相切时立即沿原路按原速返回,当⊙O回到出发时的位置(即再次与AB相切)时停止移动,已知点P与⊙O同时开始移动,同时停止移动(即同时到达各自的终止位置).
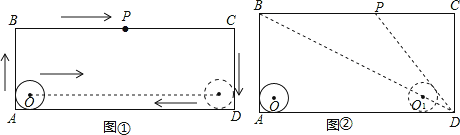
(1)如图①,点P从A→B→C→D,全程共移动了 cm(用含a、b的代数式表示);
(2)如图①,已知点P从A点出发,移动2s到达B点,继续移动3s,到达BC的中点,若点P与⊙O的移动速度相等,求在这5s时间内圆心O移动的距离;
(3)如图②,已知a=20,b=10,是否存在如下情形:当⊙O到达⊙O1的位置时(此时圆心O1在矩形对角线BD上),DP与⊙O1恰好相切?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商品原价800元,连续两次降价a%后售价为578元,下列所列方程正确的是( )
A. 800(1+a%)2=578 B. 800(1-a%)2="578" C. 800(1-2a%)=578 D. 800(1-a2%)=578
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列选项中,给出的三条线段不能组成三角形的是 ( )
A. a+1,a+2,a+3B. 三边之比为2:3:4C. 30cm,8cm ,10cmD. 3k ,4k ,5k
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的是
A. 等腰三角形一腰的长至少要大于底边长的一半
B. 三角形按边的关系分为不等边三角形、等边三角形
C. 长度为5、6、10的三条线段不能组成三角形
D. 等腰三角形的两边长是1和2,则其周长为4或5
相关试题

