【题目】(8分)一只小虫从某点P出发,在一条直线上来回爬行,假定把向右爬行的路程记为正数,向左爬行的路程记为负数,则爬行各段路程(单位:cm)依次为: ![]() .
.
(1)通过计算说明小虫是否能回到起点P.
(2)如果小虫爬行的速度为0.5cm/s,那么小虫共爬行了多长时间?
参考答案:
【答案】小虫能回到起点![]() ;小虫一共爬行了108秒.
;小虫一共爬行了108秒.
【解析】试题分析:(1)把记录到得所有的数字相加,看结果是否为0即可;
(2)记录到得所有的数字的绝对值的和,除以0.5即可.
试题解析:(1)∵(+5)+(-3)+(+10)+(-8)+(-6)+(+12)+(-10),
=5-3+10-8-6+12-10,
=0,
∴小虫能回到起点P;
(2)(5+3+10+8+6+12+10)÷0.5,
=54÷0.5,
=108(秒).
答:小虫共爬行了108秒.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列长度的三条线段,能组成三角形的是( )
A.2cm,3cm,6cmB.10cm,10cm,20cm
C.5cm,20cm,10cmD.5cm,6cm,10cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】“囧”(jiǒng)是网络的一个流行语,像一个人脸郁闷的神情,如图所示,一张边长为20的正方形纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别为
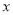 、
、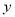 ,剪去的两个小直角三角形的两直角边长也分别为
,剪去的两个小直角三角形的两直角边长也分别为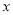 、
、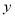 .
.(1)用含有
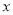 、
、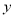 的式子表示图中“囧”的面积.
的式子表示图中“囧”的面积.(2)当
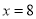 、
、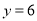 时,求此时“囧”的面积.
时,求此时“囧”的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2+x+6=0的根的情况是( )
A. 有两个相等的实数根 B. 有两个不相等的实数根
C. 只有一个实数根 D. 没有实数根
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知点P的坐标为(3,4),点P与点Q关于y轴对称,则Q点的坐标是( )
A.(3,4)
B.(-3,4)
C.(3,-4)
D.(-3,-4) -
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的方程x2-bx+6=0的一根是x=2,则另一根是( )
A.x=-3B.x=-2C.x=2D.x=3
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.
小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;
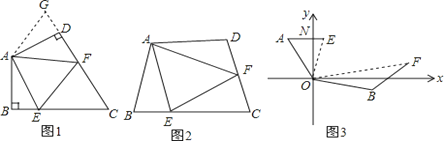
(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF=
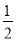 ∠BAD上述结论是否仍然成立,并说明理由;
∠BAD上述结论是否仍然成立,并说明理由;(3)如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.
相关试题

