【题目】如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
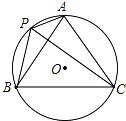
(1)判断△ABC的形状: ;
(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论.
参考答案:
【答案】(1)△ABC是等边三角形;(2)CP=BP+AP.
【解析】
试题分析:(1)利用圆周角定理可得∠BAC=∠CPB,∠ABC=∠APC,而∠APC=∠CPB=60°,所以∠BAC=∠ABC=60°,从而可判断△ABC的形状;
(2)在PC上截取PD=AP,则△APD是等边三角形,然后证明△APB≌△ADC,证明BP=CD,即可证得.
证明:(1)△ABC是等边三角形.
证明如下:在⊙O中,
∵∠BAC与∠CPB是![]() 对的圆周角,∠ABC与∠APC是
对的圆周角,∠ABC与∠APC是![]() 所对的圆周角,
所对的圆周角,
∴∠BAC=∠CPB,∠ABC=∠APC,
又∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°,
∴△ABC为等边三角形;
故答案为:△ABC是等边三角形;
(2)在PC上截取PD=AP,如图1,
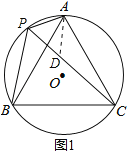
又∵∠APC=60°,
∴△APD是等边三角形,
∴AD=AP=PD,∠ADP=60°,即∠ADC=120°.
又∵∠APB=∠APC+∠BPC=120°,
∴∠ADC=∠APB,
在△APB和△ADC中,
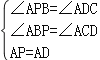 ,
,
∴△APB≌△ADC(AAS),
∴BP=CD,
又∵PD=AP,
∴CP=BP+AP.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着居民经济收入的不断提高以及汽车业的快速发展,家用汽车已越来越多地进入普通家庭,抽样调查显示,截止2015年底某市汽车拥有量为16.9万辆.己知2013年底该市汽车拥有量为10万辆,设2013年底至2015年底该市汽车拥有量的平均增长率为x,根据题意列方程得( )
A.10(1+x)2=16.9 B.10(1+2x)=16.9
C.10(1﹣x)2=16.9 D.10(1﹣2x)=16.9
-
科目: 来源: 题型:
查看答案和解析>>【题目】判断一元二次方程x2﹣2x+1=0的根的情况是( )
A.只有一个实数根 B.有两个相等的实数根
C.有两个不相等的实数根 D.没有实数根
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个三角形的两边长为3和6,若第三边取奇数,则此三角形的周长为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(﹣p)2(﹣p)3=__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂一月份生产某机器100台,计划三月份生产160台.设二、三月份每月的平均增长率为x,根据题意列出的方程是 .
-
科目: 来源: 题型:
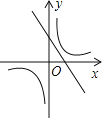
查看答案和解析>>【题目】如图,已知关于x的函数y=k(x﹣1)和y=
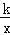 (k≠0),它们在同一坐标系内的图象大致是( )
(k≠0),它们在同一坐标系内的图象大致是( )A.
 B.
B.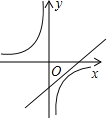 C.
C.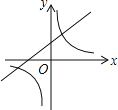 D.
D.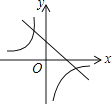
相关试题

