【题目】如图,在10×10的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线l对称的△A1B1C1;(要求:A与A1,B与B1,C与C1相对应)
(2)在(1)问的结果下,连接BB1,CC1,求四边形BB1C1C的面积.

参考答案:
【答案】解:(1)如图,△A1B1C1 是△ABC关于直线l的对称图形。

(2)由图得四边形BB1C1C是等腰梯形,BB1=4,CC1=2,高是4。
∴S四边形BB1C1C![]() 。
。
【解析】(1)关于轴对称的两个图形,各对应点的连线被对称轴垂直平分.作BM⊥直线l于点M,并延长到B1,使B1M=BM,同法得到A,C的对应点A1,C1,连接相邻两点即可得到所求的图形。
(2)由图得四边形BB1 C1C是等腰梯形,BB1=4,CC1=2,高是4,根据梯形的面积公式进行计算即可。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.
(1)求证:△ADE≌△CBF;
(2)求证:四边形BFDE为矩形.

-
科目: 来源: 题型:
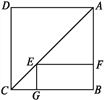
查看答案和解析>>【题目】如图,点E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,垂足分别为E,F,若正方形ABCD的周长是40 cm.
(1)求证:四边形BFEG是矩形;
(2)求四边形EFBG的周长;
(3)当AF的长为多少时,四边形BFEG是正方形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某城市按以下规定收取每月的水费,用水不超过7吨,按每吨1.5元收费;若超过7吨,未超过部分仍按每吨1.5元收取,而超过部分则按每吨2.3元收费.
(1)如果某用户5月份水费平均为每吨1.6元,那么该用户5月份应交水费多少元?
(2)如果某用户5月份交水费17.4元,那么该用户5月份水费平均每吨多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)操作发现:
如图,在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G.猜想线段GF与GC有何数量关系?并证明你的结论.

(2)类比探究:
如图,将(1)中的矩形ABCD改为平行四边形,其它条件不变,(1)中的结论是否仍然成立?请说明理由.

-
科目: 来源: 题型:
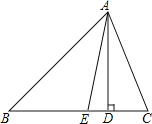
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=15°,∠B=40°.
(1)求∠C的度数.
(2)若:∠EAD=α,∠B=β,其余条件不变,直接写出用含α,β的式子表示∠C的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了选拔学生参加“汉字听写大赛”,对九年级一班、二班各10名学生进行汉字听写测试.计分采用10分制(得分均取整数),成绩达到6分或6分以上为及格,得到9分为优秀,成绩如表1所示,并制作了成绩分析表(表2).
表1
一班
5
8
8
9
8
10
10
8
5
5
二班
10
6
6
9
10
4
5
7
10
8
表2
班级
平均数
中位数
众数
方差
及格率
优秀率
一班
7.6
8
a 3.82
70%
30%
二班
b
7.5
10
4.94
80%
40%
(1)在表2中,a= ,b= ;
(2)有人说二班的及格率、优秀率均高于一班,所以二班比一班好;但也有人认为一班成绩比二班好,请你给出坚持一班成绩好的两条理由;
(3)一班、二班获满分的中同学性别分别是1男1女、2男1女,现从这两班获满分的同学中各抽1名同学参加“汉字听写大赛”,用树状图或列表法求出恰好抽到1男1女两位同学的概率.
相关试题

