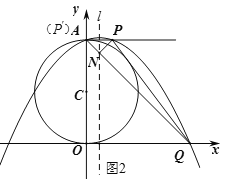
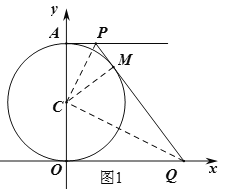
【题目】如图,在平面直角坐标系中,以点C(0,4)为圆心,半径为4的圆交y轴正半轴于点A,AB是⊙C的切线.动点P从点A开始沿AB方向以每秒1个单位长度的速度运动,点Q从O点开始沿x轴正方向以每秒4个单位长度的速度运动,且动点P、Q从点A和点O同时出发,设运动时间为t(秒).
(1)当t=1时,得到P1、Q1,求经过A、P1、Q1三点的抛物线解析式及对称轴l;
(2)当t为何值时,直线PQ与⊙C相切?并写出此时点P和点Q的坐标;
(3)在(2)的条件下,抛物线对称轴l上存在一点N,使NP+NQ最小,求出点N的坐标并说明理由.
【答案】(1)y=![]() , l:x=
, l:x=![]() ;(2)t=2时,PQ与⊙C相切,P(2,8),Q(8,0);(3)N(1,7),理由见解析.
;(2)t=2时,PQ与⊙C相切,P(2,8),Q(8,0);(3)N(1,7),理由见解析.
【解析】
(1)先求出t=1时P1,Q1的坐标,然后用待定系数法即可得出抛物线的解析式,进而可求出对称轴l的解析式;
(2)当直线PQ与圆C相切时,连接CP,CQ,根据平行线的性质、角平分线的性质和三角形的内角和可得∠PCQ=90°,则有Rt△CMP∽Rt△QMC(M为PQ与圆C的切点),然后根据相似三角形的性质即可求出t的值;
(3)本题是典型的“将军饮马”问题,解题的关键是确定N的位置,可先利用待定系数法求出此时抛物线的解析式,然后作出P点关于直线l的对称点P′的坐标,连接P′Q,那么P′Q与直线l的交点即为所求的N点,至此只要求出直线P′Q的解析式,即可求出N点的坐标,问题即得解决.
解:(1)当t=1时,AP1=1,OQ1=4,则A、P1、Q1的坐标分别为A(0,8)、P1(1,8)、Q1(4,0),
设所求抛物线解析式为y=ax2+bx+c,则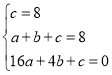 ,解得:
,解得: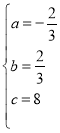
∴抛物线的解析式为y=![]() ,对称轴为直线l:x=
,对称轴为直线l:x=![]() ;
;
(2)设PQ与⊙C相切于点M,如图1,连接CP、CM、CQ,则PA=PM=t,QO=QM=4t,
∵CP、CQ分别平分∠APQ和∠OQP,∴![]() ,
,![]() ,
,
∵∠APQ+∠OQP=180°,∴∠CPQ+∠CQP=90°,
∴∠PCQ=![]() =90°,
=90°,
∵CM⊥PQ,∴可得Rt△CMP∽Rt△QMC,
∴![]() ,即
,即![]() ,∴t=±2,
,∴t=±2,
由于时间t只能取正数,所以t=2,即当运动时间t=2秒时,PQ与⊙C相切.
此时:P(2,8),Q(8,0);
(3)∵A(0,8),P(2,8),Q(8,0),∴设此时抛物线的解析式为![]() ,
,
把A,P,Q代入,得: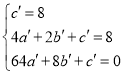 ,解得:
,解得: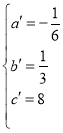 ,
,
∴抛物线的解析式为:y=![]() ,此时抛物线的对称轴为直线l:x=1,
,此时抛物线的对称轴为直线l:x=1,
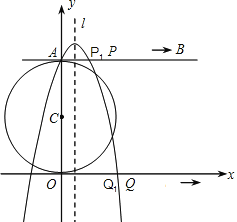
作点P关于直线l的对称点P',如图2,则P'(0,8),即为点A,设P'Q与直线x=1交于点N,则此时NP+NQ最小,
∵P'(0,8),Q(8,0),∴直线P'Q的解析式为:y=﹣x+8,当x=1时,y=﹣1+8=7.
因此N点的坐标为(1,7).