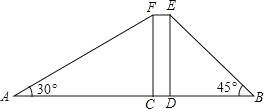
【题目】宾哥和君哥在华润广场前感慨楼房真高.君哥说:“这楼起码20层!”宾哥不以为然:“20层?我看没有,数数就知道了!”君哥说:“老大,不有办法不用数就知道吗?”宾哥想了想说:“没问题!让我们量一量把!”君哥、宾哥在楼体两侧各选A、B两点,其中CDEF表示楼体,AB=200米,CD=20米.∠A=30°,∠B=45°,(A、C、D、E四点在同一直线上)问:
(1)楼高多少米?(用含根号的式子表示)
(2)若每层楼按3米计算,你支持宾哥还是君哥的观点呢?请说明理由.(精确到0.1,参考数据:![]() ≈1.73,
≈1.73,![]() ≈1.41,
≈1.41,![]() ≈2.24)
≈2.24)
参考答案:
【答案】(1)楼高90(![]() -1)米.(2)我支持君哥的观点,这楼起码20层.
-1)米.(2)我支持君哥的观点,这楼起码20层.
【解析】
试题分析:(1)设楼高为x,则CF=DE=x,在Rt△ACF和Rt△DEB中分别用x表示AC、BD的值,然后根据AC+CD+BD=200,求出x的值即可;
(2)根据(1)求出楼高x,然后求出20层楼的高度,比较x和20层楼高的大小即可判断谁的观点正确.
试题解析:(1)设楼高为x米,则CF=DE=x米,
∵∠A=30°,∠B=45°,∠ACF=∠BDE=90°,
∴AC=![]() x米,BD=x米,
x米,BD=x米,
∴![]() x+x=200-20,
x+x=200-20,
解得x=90(![]() -1)(米),
-1)(米),
答:楼高90(![]() -1)米.
-1)米.
(2)∵x=90(![]() -1)≈90(1.73-1)=90×0.73=65.7米>3×20米,
-1)≈90(1.73-1)=90×0.73=65.7米>3×20米,
∴我支持君哥的观点,这楼起码20层.
-
科目: 来源: 题型:
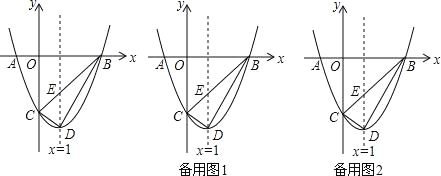
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点A、C的坐标分别为(-1,0),(0,-3),直线x=1为抛物线的对称轴.点D为抛物线的顶点,直线BC与对称轴相较于点E.
(1)求抛物线的解析式并直接写出点D的坐标;
(2)点P为直线x=1右方抛物线上的一点(点P不与点B重合).记A、B、C、P四点所构成的四边形面积为S,若S=
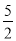 S△BCD,求点P的坐标;
S△BCD,求点P的坐标;(3)点Q是线段BD上的动点,将△DEQ延边EQ翻折得到△D′EQ,是否存在点Q使得△D′EQ与△BEQ的重叠部分图形为直角三角形?若存在,请求出BQ的长,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,C、G是⊙O上两点,且C是弧AG的中点,过点C的直线CD⊥BG的延长线于点D,交BA的延长线于点E,连接BC,交OD于点F.
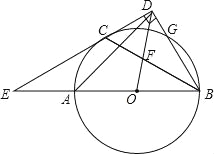
(1)求证:CD是⊙O的切线;
(2)若
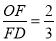 ,求证:AE=AO;
,求证:AE=AO;(3)连接AD,在(2)的条件下,若CD=2
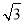 ,求AD的长.
,求AD的长. -
科目: 来源: 题型:
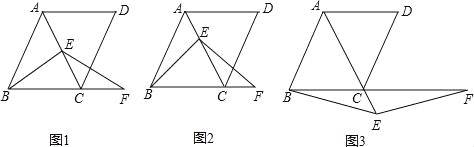
查看答案和解析>>【题目】如图,在菱形ABCD中,∠ABC=60°,E是对角线AC上任意一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.
(1)如图1,当E是线段AC的中点,且AB=2时,求△ABC的面积;
(2)如图2,当点E不是线段AC的中点时,求证:BE=EF;
(3)如图3,当点E是线段AC延长线上的任意一点时,(2)中的结论是否成立?若成立,请给予证明;若不成立,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分8分)东台沿海高速公路养护小组,乘车沿南北向公路巡视维护,如果约定向北为正,向南为负, 当天的行驶记录如下:(单位:km)
+17,-9,+7,-15,-3,+11,-6,-8,+5,+16
(1) 养护小组最后到达的地方在出发点的哪个方向?距出发点多远?
(2) 养护过程中,最远处离出发点有多远?
(3) 若汽车耗油为0.5L/km,则这次养护共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】大于﹣4.8而小于2.5的整数共有( )
A. 7个 B. 6个 C. 5个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列语句正确的是( )
A. 相似图形一定是位似图形,位似图形一定是相似图形
B. 位似图形一定是相似图形,而且位似比等于相似比
C. 利用位似变换只能放大图形,不能缩小图形
D. 利用位似变换只能缩小图形,不能放大图形
相关试题

