【题目】如图所示,数轴上有A、B、C三点,且AB=3BC,若B为原点,A点表示数为6.
(1)求C点表示的数;
(2)若数轴上有一动点P,以每秒1个单位的速度从点C向点A匀速运动,设运动时间为t秒,请用含t的代数式表示PB的长;
(3)在(2)的条件下,点P运动的同时有一动点Q从点A以每秒2个单位的速度向点C匀速运动,当P、Q两点相距2个单位长度时,求t的值.

参考答案:
【答案】(1)﹣2(2)若0<t<2时,PB的长为:2﹣t;若t>2时,PB的长为:t﹣2(3)![]() s
s
【解析】
(1)根据AB=3BC,若B为原点,A点表示数为6,即可求出C点表示的数;
(2)设运动时间为t秒,分0<t<2时,t>2时,两种情况分别求得PB的长;
(3)首先求出AC的长度,根据P从点C向点A匀速运动,Q点A向点C匀速运动,求出t的值.
(1)∵AB=3BC,A点表示数为6,若B为原点,
∴C点表示的数为﹣2.
(2)设运动时间为t秒,
若0<t<2时,PB的长为:2﹣t
若t>2时,PB的长为:t﹣2
(3)AC=AB+BC=6+2=8
∵动点P从点C向点A匀速运动,动点Q点A向点C匀速运动
∴(8+2)÷(2+1)=![]() s
s
∴t的值为![]() s.
s.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有一组有规律排列的数:1、﹣1、
 、﹣
、﹣ 、
、 、﹣
、﹣ 、1、﹣1、
、1、﹣1、 、﹣
、﹣ 、
、 、﹣
、﹣ …其中,1、﹣1、
…其中,1、﹣1、 、﹣
、﹣ 、
、 、﹣
、﹣ 这六个数按此规律重复出现,问:
这六个数按此规律重复出现,问:(1)第50个数是什么数?
(2)把从第1个数开始的前2017个数相加,结果是多少?
(3)从第1个数起,把连续若干个数的平方加起来,如果和为520,则共有多少个数的平方相加?
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们来定义一种新运算:对于任意实数x、y,“※”为a※b=(a+1)(b+1)﹣1
(1)计算(﹣3)※9
(2)嘉琪研究运算“※”之后认为它满足交换律,你认为她的判断 (正确、错误)
(3)请你帮助嘉琪完成她对运算“※”是否满足结合律的证明.
证明:由已知把原式化简得a※b=(a+1)(b+1)﹣1=ab+a+b
∵(a※b)※c=(ab+a+b)※c=
a※(b※c)=
∴
∴运算“※”满足结合律.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=﹣
 x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为
x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为  m.
m. 
(1)求该抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上有A、B、C、D四个点,分别对应的数为a,b,c,d,且满足a,b是方程|x+7|=1的两个解(a<b),且(c﹣12)2与|d﹣16|互为相反数.
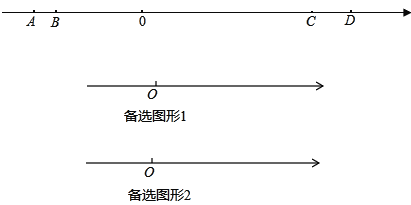
(1)填空:a= 、b= 、c= 、d= ;
(2)若线段AB以3个单位/秒的速度向右匀速运动,同时线段CD以1单位长度/秒向左匀速运动,并设运动时间为t秒,A、B两点都运动在CD上(不与C,D两个端点重合),若BD=2AC,求t得值;
(3)在(2)的条件下,线段AB,线段CD继续运动,当点B运动到点D的右侧时,问是否存在时间t,使BC=3AD?若存在,求t得值;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于
 MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )①AD是∠BAC的平分线 ②∠ADC=60°
③点D在AB的垂直平分线上 ④AB=2AC.

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程,是一元二次方程的是( )
①3x2+x=20,②2x2﹣3xy+4=0,③x2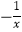 =4,④x2=0,⑤x2﹣3x﹣4=0.
=4,④x2=0,⑤x2﹣3x﹣4=0.
A.①②
B.①②④⑤
C.①③④
D.①④⑤
相关试题

