【题目】如图,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD、等边△ACE、等边△BCF.证明四边形DAEF是平行四边形.

参考答案:
【答案】见解析
【解析】试题分析:根据已知条件易证△ABC≌△DBF,根据全等三角形的性质可得AC=DF;同理可证得AB=EF.即可得EF=AD,DF=AE,根据两组对边分别相等的四边形是平行四边形即可证得结论.
试题解析:
证明:∵△ABD和△BCF都是等边三角形,
∴∠DBF+∠FBA=∠ABC+∠ABF=60°,BD=BA,BF=BC,
∴∠DBF=∠ABC.
∴△ABC≌△DBF,∴AC=DF.
又∵AC=AE,∴DF=AE.
同理可证得△ABC≌△EFC,∴AB=EF.
又∵AB=AD,∴EF=AD,
∴四边形DAEF是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB中点)所在的直线上,得到经过点D的折痕DE.则∠DEC的大小为( )

A.78°
B.75°
C.60°
D.45° -
科目: 来源: 题型:
查看答案和解析>>【题目】4月的某天小欣在“A超市”买了“雀巢巧克力”和“趣多多小饼干”共10包,已知“雀巢巧克力”每包22元,“趣多多小饼干”每包2元,总共花费了80元.
(1)请求出小欣在这次采购中,“雀巢巧克力”和“趣多多小饼干”各买了多少包?
(2)“五一”期间,小欣发现,A、B两超市以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在A超市累计购物超过50元后,超过50元的部分打九折;在B超市累计购物超过100元后,超过100元的部分打八折.
①请问“五一”期间,若小欣购物金额超过100元,去哪家超市购物更划算?
②“五一”期间,小欣又到“B超市”购买了一些“雀巢巧克力”,请问她至少购买多少包时,平均每包价格不超过20元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果三角形满足一个角是另一个角的3倍,那么我们称这个三角形为“智慧三角形”.下列各组数据中,能作为一个智慧三角形三边长的一组是( )
A.1,2,3
B.1,1,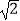
C.1,1,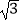
D.1,2,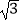
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,点D、E分别在BC、AC边上,且∠ADE=60°,AB=3,BD=1,则EC= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线y=
 x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是 .
x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
 ,并将不等式组的解集在数轴上表示出来.
,并将不等式组的解集在数轴上表示出来.
相关试题

