【题目】如图1,地面BD上两根等长立柱AB,CD之间悬挂一根近似成抛物线![]() 的绳子.
的绳子.
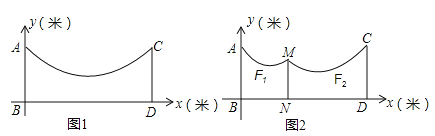
(1)求绳子最低点离地面的距离;
(2)因实际需要,在离AB为3米的位置处用一根立柱MN撑起绳子(如图2),使左边抛物线F1的最低点距MN为1米,离地面1.8米,求MN的长;
(3)将立柱MN的长度提升为3米,通过调整MN的位置,使抛物线F2对应函数的二次项系数始终为![]() ,设MN离AB的距离为m,抛物线F2的顶点离地面距离为k,当2≤k≤2.5时,求m的取值范围.
,设MN离AB的距离为m,抛物线F2的顶点离地面距离为k,当2≤k≤2.5时,求m的取值范围.
参考答案:
【答案】(1)![]() m;(2)2.1m;(3)4≤m≤
m;(2)2.1m;(3)4≤m≤![]() .
.
【解析】
试题分析:(1)直接利用配方法求出二次函数最值得出答案;
(2)利用顶点式求出抛物线F1的解析式,进而得出x=3时,y的值,进而得出MN的长;
(3)根据题意得出抛物线F2的解析式,得出k的值,进而得出m的取值范围.
试题解析:(1)∵a=![]() >0,∴抛物线顶点为最低点,∵
>0,∴抛物线顶点为最低点,∵![]() =
=![]() ,∴绳子最低点离地面的距离为:
,∴绳子最低点离地面的距离为:![]() m;
m;
(2)由(1)可知,BD=8,令x=0得y=3,∴A(0,3),C(8,3),由题意可得:抛物线F1的顶点坐标为:(2,1.8),设F1的解析式为:![]() ,将(0,3)代入得:4a+1.8=3,解得:a=0.3,∴抛物线F1为:
,将(0,3)代入得:4a+1.8=3,解得:a=0.3,∴抛物线F1为:![]() ,当x=3时,y=0.3×1+1.8=2.1,∴MN的长度为:2.1m;
,当x=3时,y=0.3×1+1.8=2.1,∴MN的长度为:2.1m;
(3)∵MN=DC=3,∴根据抛物线的对称性可知抛物线F2的顶点在ND的垂直平分线上,∴抛物线F2的顶点坐标为:(![]() ,k),∴抛物线F2的解析式为:
,k),∴抛物线F2的解析式为:![]() ,把C(8,3)代入得:
,把C(8,3)代入得:![]() ,解得:
,解得:![]() ,∴k=
,∴k=![]() ,∴k是关于m的二次函数,又∵由已知m<8,在对称轴的左侧,∴k随m的增大而增大,∴当k=2时,
,∴k是关于m的二次函数,又∵由已知m<8,在对称轴的左侧,∴k随m的增大而增大,∴当k=2时,![]() ,解得:
,解得:![]() ,
,![]() (不符合题意,舍去),当k=2.5时,
(不符合题意,舍去),当k=2.5时,![]() ,解得:
,解得:![]() ,
,![]() (不符合题意,舍去),∴m的取值范围是:4≤m≤
(不符合题意,舍去),∴m的取值范围是:4≤m≤![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B、C、E在同一条直线上,△ABC与△CDE都是等边三角形,则下列结论不一定成立的是( ).
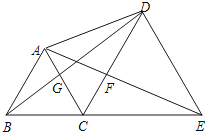
A.△ACE≌△BCD
B.△BGC≌△AFC
C.△DCG≌△ECF
D.△ADB≌△CEA -
科目: 来源: 题型:
查看答案和解析>>【题目】2016年3月国际风筝节在铜仁市万山区举办,王大伯决定销售一批风筝,经市场调研:蝙蝠型风筝进价每个为10元,当售价每个为12元时,销售量为180个,若售价每提高1元,销售量就会减少10个,请回答以下问题:
(1)用表达式表示蝙蝠型风筝销售量y(个)与售价x(元)之间的函数关系(12≤x≤30);
(2)王大伯为了让利给顾客,并同时获得840元利润,售价应定为多少?
(3)当售价定为多少时,王大伯获得利润最大,最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知两点E(x1,y1),F(x2,y2),如果x1+x2=2x1,y1+y2=0,那么E,F两点关于_______对称.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个运算程序的示意图,若开始输入的x值为81,我们看到第一次输出的结果为27,第二次输出的结果为9,…,第2017次输出的结果为( )
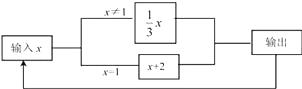
A.1
B.3
C.9
D.27 -
科目: 来源: 题型:
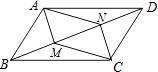
查看答案和解析>>【题目】已知:如图,在ABCD中,M、N是对角线BD上的两点,且BM=DN. 求证:四边形AMCN是平行四边形.
-
科目: 来源: 题型:
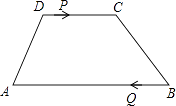
查看答案和解析>>【题目】如图,梯形ABCD中,AB∥CD,AB=24cm,DC=10cm,点P和Q同时从D、B出发,P由D向C运动,速度为每秒1cm,点Q由B向A运动,速度为每秒3cm,试求几秒后,P、Q和梯形ABCD的两个顶点所形成的四边形是平行四边形?
相关试题

