【题目】请把下面证明过程补充完整
如图,已知AD⊥BC于D,点E在BA的延长线上,EG⊥BC于C,交AC于点F,∠E=∠1.求证:AD平分∠BAC.

证明:∵AD⊥BC于D,EG⊥BC于G( ),
∴∠ADC=∠EGC=90°( ),
∴AD∥EG( ),
∴∠1=∠2( ),
∴_____=∠3( ),
又∵∠E=∠1(已知),∴∠2=∠3( ),
∴AD平分∠BAC( )
参考答案:
【答案】已知;垂直的定义;同位角相等,两直线平行;两直线平行,内错角相等;∠E;两直线平行,同位角相等;等量代换;角平分线的定义.
【解析】
已知垂直AD⊥BC于D,EG⊥BC于G,可推得∠ADC=∠EGC=90°,同位角相等可推出两条直线平行,两条直线平行可推得,内错角和同位角相等,再利用等量代换,可得AD平分∠BAC.
∵AD⊥BC于D,EG⊥BC于G(已知),
∴∠ADC=∠EGC=90°( 垂直的定义),
∴AD∥EG( 同位角相等,两直线平行),
∴∠1=∠2( 两直线平行,内错角相等),
∴∠E=∠3( 两直线平行,同位角相等),
又∵∠E=∠1(已知),
∴∠2=∠3( 等量代换),
∴AD平分∠BAC( 角平分线的定义).
-
科目: 来源: 题型:
查看答案和解析>>【题目】经市场调查,某种商品在第x天的售价与销量的相关信息如下表;已知该商品的进价为每件30元,设销售该商品每天的利润为y元.
(1)求出y与x的函数关系式
(2)问销售该商品第几天时,当天销售利润最大?最大利润是多少? .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】ABCD中,E是CD边上一点,
(1)将△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,如图1所示.观察可知:与DE相等的线段是 , ∠AFB=∠ .
(2)如图2,正方形ABCD中,P、Q分别是BC、CD边上的点,且∠PAQ=45°,试通过旋转的方式说明:DQ+BP=PQ.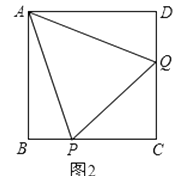
(3)在(2)题中,连接BD分别交AP、AQ于M、N,你还能用旋转的思想说明BM2+DN2=MN2 .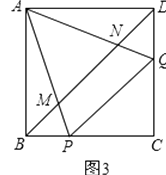
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线C1:y=x2+bx+c经过原点,与x轴的另一个交点为(2,0),将抛物线C1向右平移m(m>0)个单位得到抛物线C2 , C2交x轴于A,B两点(点A在点B的左边),交y轴于点C.
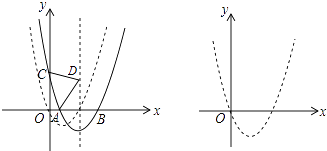
(1)求抛物线C1的解析式及顶点坐标;
(2)以AC为斜边向上作等腰直角三角形ACD,当点D落在抛物线C2的对称轴上时,求抛物线C2的解析式;
(3)若抛物线C2的对称轴存在点P,使△ PAC为等边三角形,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数与反比例函数的图象交于点P(3,m),Q(1,3).
(1)求反函数的函数关系式;
(2)在给定的直角坐标系(如图)中,画出这两个函数的大致图象;
(3)当x为何值时,一次函数的值大于反比例函数的值?

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,是轴对称图形但不是中心对称图形的是( )
A.
B.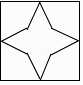
C.
D.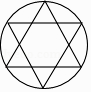
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形ABC(记作△ABC)在8×8方格中,位置如图所示,A(﹣2,1),B(﹣1,4).
(1)请你在方格中建立直角坐标系,并写出C点的坐标;
(2)把△ABC向上平移2个单位长度,再向右平移3个单位长度,请你画出平移后的△A1B1C1,若△ABC内部一点P的坐标为(a,b),则点P的对应点P1的坐标是 .
(3)在x轴上存在一点D,使△DBC的面积等于3,则点D的坐标为 .

相关试题

