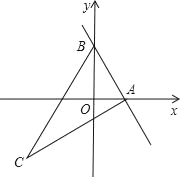
【题目】已知:如图,直线y=kx+2与x轴正半轴相交于A(t,0),与y轴相交于点B,抛物线y=﹣x2+bx+c经过点A和点B,点C在第三象象限内,且AC⊥AB,tan∠ACB=![]() .
.
(1)当t=1时,求抛物线的表达式;
(2)试用含t的代数式表示点C的坐标;
(3)如果点C在这条抛物线的对称轴上,求t的值.
参考答案:
【答案】(1)抛物线的表达式为y=﹣x2﹣x+2;(2)点C的坐标为(t﹣4,﹣2t);
(3)t=4﹣![]() .
.
【解析】试题分析:(1)把点A(1,0),B(0,2)分别代入抛物线的表达式,解方程组即可;
(2)如图:作CH⊥x轴,垂足为点H,根据△AOB∽△CHA,得到![]() ,根据tan∠ACB=
,根据tan∠ACB=![]() =
=![]() ,得到
,得到![]() =
=![]() ,根据OA=t,得到点C的坐标为(t-4,-2t).
,根据OA=t,得到点C的坐标为(t-4,-2t).
(3)根据点C(t-4,-2t)在抛物线y=-x2+bx+c的对称轴上,得到t-4=![]() ,即b=2t-8,把点A(t,0)、B(0,2)代入抛物线的表达式,得-t2+bt+2=0,可知t2+(2t-8)t+2=0,即t2-8t+2=0,据此即可求出t的值.
,即b=2t-8,把点A(t,0)、B(0,2)代入抛物线的表达式,得-t2+bt+2=0,可知t2+(2t-8)t+2=0,即t2-8t+2=0,据此即可求出t的值.
试题解析:
(1)∵t=1,y=kx+2,
∴A(1,0),B(0,2),
把点A(1,0),B(0,2)分别代入抛物线的表达式,得![]() ,
,
解得![]() ,
,
∴所求抛物线的表达式为y=﹣x2﹣x+2.
(2)如图:作CH⊥x轴,垂足为点H,得∠AHC=∠AOB=90°,
∵AC⊥AB,
∴∠OAB+∠CAH=90°,
又∵∠CAH+∠ACH=90°,
∴∠OAB=∠ACH,
∴△AOB∽△CHA,
∴![]() ,
,
∵tan∠ACB=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵OA=t,OB=2,
∴CH=2t,AH=4,
∴点C的坐标为(t﹣4,﹣2t).
(3)∵点C(t﹣4,﹣2t)在抛物线y=﹣x2+bx+c的对称轴上,
∴t﹣4=![]() ,即b=2t﹣8,
,即b=2t﹣8,
把点A(t,0)、B(0,2)代入抛物线的表达式,得﹣t2+bt+2=0,
∴﹣t2+(2t﹣8)t+2=0,即t2﹣8t+2=0,
解得t=4+![]() ,
,
∵点C(t﹣4,﹣2t)在第三象限,
∴t=4+![]() 不符合题意,舍去,
不符合题意,舍去,
∴t=4﹣![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于50%.经试销发现,销售量P(件)与销售单价x(元)符合一次函数关系,当销售单价为65元时销售量为55件,当销售单价为75元时销售量为45件.
(Ⅰ)求P与x的函数关系式;
(Ⅱ)若该商场获得利润为y元,试写出利润y与销售单价x之间的关系式;
(Ⅲ)销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O为原点,点A(1,0),点B(0,
 ),把△ABO绕点O顺时针旋转,得A′B′O,记旋转角为α.
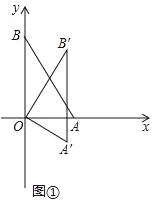
),把△ABO绕点O顺时针旋转,得A′B′O,记旋转角为α.(Ⅰ)如图①,当α=30°时,求点B′的坐标;
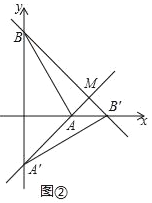
(Ⅱ)设直线AA′与直线BB′相交于点M.
如图②,当α=90°时,求点M的坐标;
②点C(﹣1,0),求线段CM长度的最小值.(直接写出结果即可)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,
 的顶点均在格点上,点
的顶点均在格点上,点 的坐标为
的坐标为 .
.
①把
 向上平移5个单位后得到对应的
向上平移5个单位后得到对应的 ,画出
,画出 ,并写出
,并写出 的坐标;
的坐标;②以原点
 为对称中心,画出
为对称中心,画出 与关于原点
与关于原点 对称的
对称的 ,并写出点
,并写出点 的坐标.
的坐标.③以原点O为旋转中心,画出把
 顺时针旋转90°的图形△A3B3C3,并写出C3的坐标.
顺时针旋转90°的图形△A3B3C3,并写出C3的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上
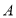 点表示数
点表示数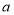 ,
, 点表示数
点表示数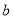 ,
,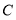 点表示数
点表示数 ,已知数
,已知数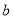 是最小的正整数,且
是最小的正整数,且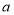 、
、 满足
满足 .
.
(1)
 ,
,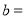 ,
, ;
;(2)若将数轴折叠,使得点
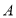 与点
与点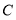 重合,则点
重合,则点 与数 表示的点重合;
与数 表示的点重合;(3)点
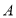 、
、 、
、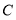 开始在数轴上运动,若点
开始在数轴上运动,若点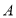 以每秒1个单位长度的速度向左运动,同时,点
以每秒1个单位长度的速度向左运动,同时,点 和点
和点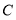 分别以每秒2个单位长度和4个单位长度的速度向右运动,假设
分别以每秒2个单位长度和4个单位长度的速度向右运动,假设 秒钟过后,若点
秒钟过后,若点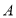 与点
与点 之间的距离表示为
之间的距离表示为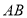 ,点
,点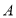 与点
与点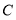 之间的距离表示为
之间的距离表示为 ,点
,点 与点
与点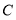 之间的距离表示为
之间的距离表示为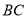 ,求
,求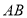 、
、 、
、 的长(用含
的长(用含 的式子表示);
的式子表示);(4)在(3)的条件下,
 的值是否随着时间
的值是否随着时间 的变化而改变?若改变,请说明理由;若不变,请求其值.
的变化而改变?若改变,请说明理由;若不变,请求其值. -
科目: 来源: 题型:
查看答案和解析>>【题目】由于受到手机更新换代的影响,某手机店经销的甲型号手机二月份售价比一月份售价每台降价500元.如果卖出相同数量的甲型号手机,那么一月份销售额为9万元,二月份销售额只有8万元.
(1)一月份甲型号手机每台售价为多少元?
(2)为了提高利润,该店计划三月份加入乙型号手机销售,已知甲型号每台进价为3500元,乙型号每台进价为4000元,预计用不多于7.6万元且不少于7.4万元的资金购进这两种手机共20台,请问有几种进货方案?
-
科目: 来源: 题型:
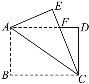
查看答案和解析>>【题目】如图,在矩形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长等于( )
A.
 B.
B.  C.
C.  D.
D. 
相关试题

