【题目】如图,已知A、B、C分别是⊙O上的点,∠B=60°,P是直径CD的延长线上的一点,且AP=AC.
(1)求证:AP与⊙O相切;
(2)如果PD=![]() ,求AP的长.
,求AP的长.

参考答案:
【答案】(1)证明参见解析;(2)3.
【解析】
试题分析:(1)利用圆周角定理以及等腰三角形的性质,得出∠P=∠ACP=∠OCA=∠OAC=30°,∠PAC=120°,进而得出∠PAO=90°,即可得出答案;(2)首先根据直角三角形中30°角所对的直角边等于斜边的一半求得半径,从而求得OA、OP,进而利用勾股定理得出AP的长.
试题解析:(1)如图:连接AO,
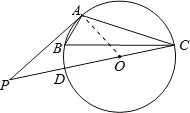 ∵∠B=60°,∴∠AOC=120°,∵AO=CO,AP=AC,∴∠P=∠ACP,∠OCA=∠OAC=30°,∴∠P=∠ACP=∠OCA=∠OAC=30°,∴∠PAC=120°,∴∠PAO=90°,∴AP是⊙O的切线;(2)设⊙O的半径为R,则OA=OD=R,PD=
∵∠B=60°,∴∠AOC=120°,∵AO=CO,AP=AC,∴∠P=∠ACP,∠OCA=∠OAC=30°,∴∠P=∠ACP=∠OCA=∠OAC=30°,∴∠PAC=120°,∴∠PAO=90°,∴AP是⊙O的切线;(2)设⊙O的半径为R,则OA=OD=R,PD=![]() ,∴OP=
,∴OP=![]() +R,∵∠PAO=90°,∠P=30°,∴OP=2OA,即
+R,∵∠PAO=90°,∠P=30°,∴OP=2OA,即![]() +R=2R,解得R=
+R=2R,解得R=![]() ,∴OA=
,∴OA=![]() ,OP=2
,OP=2![]() ,根据勾股定理得:PA=
,根据勾股定理得:PA=![]() ,AP=
,AP=![]() =
=![]() =3.故AP长为3.
=3.故AP长为3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P为反比例函数y=
 (x>0)图象上一点,以点P为圆心作圆,且该圆恰与两坐标轴都相切.在y轴任取一点E,连接PE并过点P作直线PE的垂线与x轴交于点F,则线段OE与线段OF的长度可能满足的数量关系式是 .
(x>0)图象上一点,以点P为圆心作圆,且该圆恰与两坐标轴都相切.在y轴任取一点E,连接PE并过点P作直线PE的垂线与x轴交于点F,则线段OE与线段OF的长度可能满足的数量关系式是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.(2a)2=2a2
B.a6÷a2=a3
C.(a+b)2=a2+b2
D.a3a2=a5 -
科目: 来源: 题型:
查看答案和解析>>【题目】若a+b=3,则a2﹣b2+6b=_____;若2x+5y﹣3=0,则4x32y=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果x<0,且|x|=4,则x-1=_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市出租车起步价是5元(3公里及3公里以内为起步价),以后每公里收费是1.6元,不足1公里按1公里收费,小明乘出租车到达目的地时计价器显示为11.4元,则此出租车行驶的路程可能为( )
A. 5.5公里 B. 6.9公里 C. 7.5公里 D. 8.1公里
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:一次函数的图象与y轴交于C(0,4),且与反比例函数y=
 (x>0)的图象在第一象限内交于A(3.a),B(1,b)两点.
(x>0)的图象在第一象限内交于A(3.a),B(1,b)两点.(1)求△A0C的面积;
(2)若
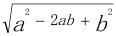 =2,求反比例函数和一次函数的解析式.
=2,求反比例函数和一次函数的解析式.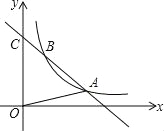
相关试题

