搜索
【题目】下列三角函数值最大的是（ ）
A.tan46°
B.sin50°
C.cos50°
D.sin40°
参考答案：
【答案】A
【解析】解：∵tan46°＞tan45°＞1；而任何锐角的正弦，余弦值都小于1；
∴最大的是：tan46°
故选A．
【考点精析】关于本题考查的锐角三角函数的增减性，需要了解当角度在0°~90°之间变化时：（1）正弦值随着角度的增大（或减小）而增大（或减小）（2）余弦值随着角度的增大（或减小）而减小（或增大）（3）正切值随着角度的增大（或减小）而增大（或减小）（4）余切值随着角度的增大（或减小）而减小（或增大）才能得出正确答案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，以平行四边形ABCD的边CD为斜边向内作等腰直角△CDE，使AD=DE=CE，∠DEC=90°，且点E在平行四边形内部，连接AE、BE，则∠AEB的度数是（ ）
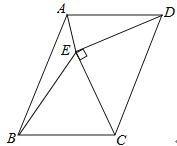
A.120°
B.135°
C.150°
D.45° -
科目： 来源： 题型：
查看答案和解析>>【题目】两圆的直径分别为4和6，若两圆有唯一公共点，这两圆的圆心距是______．
-
科目： 来源： 题型：
查看答案和解析>>【题目】邮递员骑车从邮局O出发，先向西骑行2km到达A村，继续向西骑行3km到达B村，然后向东骑行8km，到达C村，最后回到邮局.
（1）以邮局为原点，以向东方向为正方向，用1cm表示1km，画出数轴，并在该数轴上表示出A、B、C三个村庄的位置；
（2）C村距离A村有多远？
（3）邮递员共骑行了多少km？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF、CF，则下列结论：（1）∠DCF=
∠BCD，（2）EF=CF；（3）S△BEC=2S△CEF；（4）∠DFE=3∠AEF，其中正确结论的个数是（ ）
A.1个
B.2个
C.3个
D.4个 -
科目： 来源： 题型：
查看答案和解析>>【题目】小明同学用长分别为5，7，9，13(单位：厘米)的四根木棒摆三角形，用其中的三根
首尾顺次相接，每摆好一个后，拆开再摆，这样可摆出不同的三角形的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】目前甲型H1N1流感病毒在全球已有蔓延趋势，世界卫生组织提出各国要严加防控，因为曾经有一种流感病毒，若一人患了流感，经过两轮传染后共有81人患流感．如果设每轮传染中平均一个人传染x个人，那么可列方程为______．
相关试题
