【题目】(本小题满分7分)“保护环境,人人有责”,为了了解某市的空气质量情况,某校环保兴趣小组,随机抽取了2014年内该市若干天的空气质量情况作为样本进行统计,绘制了如图所示的条形统计图和扇形统计图(部分信息未给出).
请你根据图中提供的信息,解答下列问题:

(1)补全条形统计图;
(2)估计该市这一年(365天)空气质量达到“优”和“良”的总天数;
(3)计算随机选取这一年内的某一天,空气质量是“优”的概率.
参考答案:
【答案】(2)292天(3)![]()
【解析】
试题分析:(1)根据轻度污染的天数为3天,占得百分比为5%,可求得总天数为3÷5%=60天,然后用总的减去已知的可求得轻微污染的天数为60-54=6天,然后可补全条形统计图;
(2)先求出样本中优良的总天数为48天,可求得二者占样本的百分数,然后用总数乘以百分数即可;
(3)用样本中优的天数除以样本的总天数可求得概率.
试题解析:解:(1)图形补充正确.

(2)方法一:由(1)知样本容量是60,
∴该市2014年(365天)空气质量达到“优”、“良”的总天数约为:
![]() (天).
(天).
方法二:由(1)知样本容量是60,
∴该市2014年(365天)空气质量达到“优”的天数约为:
![]() (天).
(天).
该市2014年(365天)空气质量达到“良”的天数约为:
![]() (天).
(天).
∴该市2014年(365天)空气质量达到“优”、“良”的总天数约为:
73+219=292(天).
(3)随机选取2014年内某一天,空气质量是“优”的概率为:
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(a2-1)0=1,则a的取值范围是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道有两条边相等的三角形叫做等腰三角形.类似的,我们定义:至少有一组对边相等的四边形叫做等对边四边形.
(1)请写出一个你学过的四边形中是等对边四边形的图形的名称.
(2)如图1,在
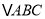 中,点
中,点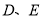 分别在
分别在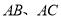 上,且
上,且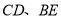 相交于点
相交于点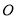 ,若
,若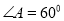 ,
, 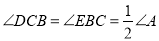 .请你写出与
.请你写出与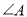 相等的角.
相等的角.(3)我们易证图中的四边形
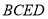 是等对边四边形.
是等对边四边形.(提示:如图2,可证
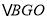 ≌
≌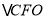 再证
再证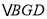 ≌
≌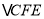 ,可得到结论
,可得到结论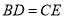 .不需证明)
.不需证明)若在
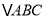 中,如果
中,如果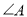 是不等于
是不等于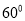 的锐角,
的锐角, 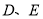 分别在
分别在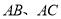 上,且
上,且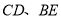 相交于点
相交于点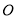 ,
, 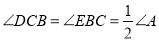 .探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.
.探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.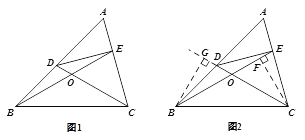
-
科目: 来源: 题型:
查看答案和解析>>【题目】一批货物要运往某地,货主准备租用汽车运输公司的甲、乙两种货车,已知过去租用这两种货车情况如下:
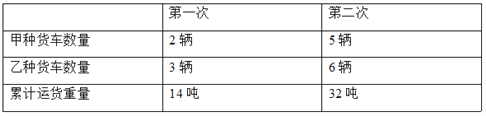
(1)分别求甲、乙两种货车载重多少吨?
(2)现在租用该公司5辆甲货车和7辆乙货车一次刚好运完这批货物,如果按每吨付费50元计算,货主应付运费多少元?
-
科目: 来源: 题型:
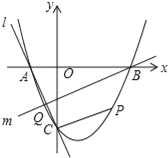
查看答案和解析>>【题目】如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)
(1)求抛物线的解析式;
(2)点P在抛物线位于第四象限的部分上运动,当四边形ABPC的面积最大时,求点P的坐标和四边形ABPC的最大面积.
(3)直线l经过A、C两点,点Q在抛物线位于y轴左侧的部分上运动,直线m经过点B和点Q,是否存在直线m,使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似?若存在,求出直线m的解析式,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是我们生活中经常接触的小刀,刀片的外壳是四边形,而且刀片外壳与刀片铆合部分都是直角,刀片的上、下是平行的,转动刀片时会形成∠1和∠2,则∠1+∠2的度数为( )

A. 80° B. 70° C. 90° D. 100°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,有一Rt△ABC,且A(﹣1,3),B(﹣3,﹣1),C(﹣3,3),已知△A1AC1是由△ABC旋转得到的.
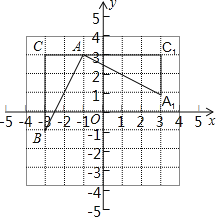
(1)请写出旋转中心的坐标是 ,旋转角是 度;
(2)以(1)中的旋转中心为中心,分别画出△A1AC1顺时针旋转90°、180°的三角形;
(3)设Rt△ABC两直角边BC=a、AC=b、斜边AB=c,利用变换前后所形成的图案证明勾股定理.
相关试题

