【题目】先化简,再求值:(3a2﹣a﹣1)﹣2(3﹣a+2a2),其中a2﹣a=2.
参考答案:
【答案】解:原式=3a2-a-1-6+2a-4a2
=-a2+a-7=-(a2-a)-7,
把a2-a=2代入得:原式=-2-7=-9
【解析】原式去括号合并得到最简结果,把a的值代入计算即可求出值. 此题考查了整式的加减,熟练掌握运算法则是解本题的关键.
【考点精析】认真审题,首先需要了解代数式求值(求代数式的值,一般是先将代数式化简,然后再将字母的取值代入;求代数式的值,有时求不出其字母的值,需要利用技巧,“整体”代入),还要掌握整式加减法则(整式的运算法则:(1)去括号;(2)合并同类项)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠A、∠B、∠C所对的边分别是a、b、c,在下列关系中,不属于直角三角形的是( )
A.b2=a2﹣c2
B.a:b:c=3:4:5
C.∠A﹣∠B=∠C
D.∠A:∠B:∠C=3:4:5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰直角三角形
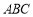 中,
中, ,
, ,
,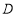 是
是 的中点,
的中点,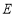 ,
,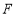 分别是
分别是 ,
,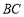 上的点(点
上的点(点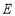 不与端点
不与端点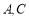 重合),且
重合),且 ,连接
,连接 并取
并取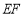 的中点
的中点 ,连接
,连接 并延长至点
并延长至点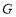 ,使
,使 ,连接
,连接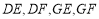 .
.
(1)求证:四边形
 是正方形;
是正方形;(2)当点
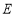 在什么位置是,四边形
在什么位置是,四边形 的面积最小?并求四边形
的面积最小?并求四边形 面积的最小值.
面积的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②3b+2c<0;③4a+c<2b;④m(am+b)+b<a(m≠1),其中结论正确的个数是( )

A.1 B.2 C.3 D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图甲,直线y=﹣x+3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.
(1)求该抛物线的解析式;
(2)在该抛物线的对称轴上是否存在点M,使以C,P,M为顶点的三角形为等腰三角形?若存在,请直接写出所符合条件的点M的坐标;若不存在,请说明理由;
(3)当0<x<3时,在抛物线上求一点E,使△CBE的面积有最大值(图乙、丙供画图探究).

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数y1=
 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).(1)求这两个函数的表达式;
(2)根据图象直接写出一次函数的值大于反比例函数的值的x的取值范围.

相关试题

